Média, Moda e Mediana
Se tivermos uma sequência de números ![a[1] .. a[n]](images/curso9_226.gif) , podendo ter repetições, a média (
Mean
) é definida como
, podendo ter repetições, a média (
Mean
) é definida como
![mu = `/`(`*`(sum(a[i], i = 1 .. n)), `*`(n))](images/curso9_227.gif)
A média também é usualmente chamada de expectância.
A moda (
Mode
) é o número que mais aparece na sequência. Por exemplo, a moda de 1,2,2,5,6 é 2. Por outro lado, a sequência 1,3,3,5,5,6 tem duas modas: 3 e 5, neste caso é a sequência é chamada bimodal. Se houver mais do que duas modas, normalmente usamos o termo multimodal e se não há repetições, usamos o termo sequência amodal (O comando
Mode
retorna todos os elementos). Uma sequência que tem uma única moda também é chamada unimodal.
A mediana (
Median
) é o valor numérico 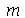 tal que metade dos números da sequência são menores do que
tal que metade dos números da sequência são menores do que 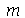 e metade dos números são maiores que
e metade dos números são maiores que 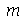 . Por exemplo, a mediana de 1,2,2,5,6,7,8 é
. Por exemplo, a mediana de 1,2,2,5,6,7,8 é 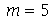 , pois três numeros (1,2,2) são menores do que 5 e três números (6,7,8) são maiores do que 5. Por outro lado, a mediana de 2,5,6,7 é
, pois três numeros (1,2,2) são menores do que 5 e três números (6,7,8) são maiores do que 5. Por outro lado, a mediana de 2,5,6,7 é 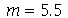 , pois como
, pois como 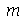 não pode estar na sequência ele é o valor médio entre 5 e 6.
não pode estar na sequência ele é o valor médio entre 5 e 6.
As definições de média, moda e mediana dadas acima usaram uma amostra de pontos, por isto, elas também são chamadas de média amostral, moda amostral e mediana amostral. Estes mesmos conceitos podem ser aplicados para variáveis aleatórias com distribuições de probabilidades discretas ou contínuas. Estas definições são estendidas devido ao contexto. Se 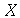 é uma variável aleatória em um espaço amostral discreto constituído pelo conjunto de pontos
é uma variável aleatória em um espaço amostral discreto constituído pelo conjunto de pontos ![a[1] .. a[n]](images/curso9_235.gif) (sem repetições,
(sem repetições, 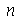 podendo ser infinito), a média
podendo ser infinito), a média 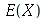 é definida como
é definida como
![E(X) = sum(`*`(P(X = a[i]), `*`(a[i])), i = 1 .. n)](images/curso9_238.gif)
onde ![P(X = a[i])](images/curso9_239.gif) é a probabilidade da variável
é a probabilidade da variável 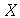 ter o valor
ter o valor ![a[i]](images/curso9_241.gif) . Se o espaço amostral é a reta real, a média é definida como
. Se o espaço amostral é a reta real, a média é definida como
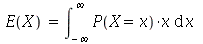
Quando o espaço amostral é a reta real, a moda é o número (ou números) na reta real cujo valor é um máximo global da distribuição de probabilidades. As vezes, máximos locais também são chamados de moda.
A mediana é definida como o valor 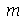 tal que
tal que
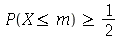 e
e 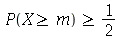
O valor de 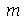 não é único necessariamente. Se
não é único necessariamente. Se 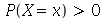 para todo
para todo 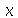 , o valor de
, o valor de 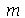 é único e geometricamente corresponde ao ponto da reta real que divide a área embaixo da curva da distribuição de probabilidades exatamente no meio.
é único e geometricamente corresponde ao ponto da reta real que divide a área embaixo da curva da distribuição de probabilidades exatamente no meio.
Por exemplo, a distribuição de probabilidades contínua 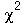 (chi-quadrado ou
ChiSquare
) com
(chi-quadrado ou
ChiSquare
) com 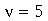 graus de liberdade tem o seguinte gráfico
graus de liberdade tem o seguinte gráfico
| > |

 |
Vamos calcular a média, moda e mediana para 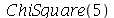 .
.
| > |
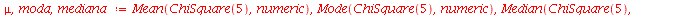
 |
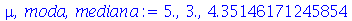 |
(2.7.1) |
| > |
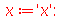 |
| > |
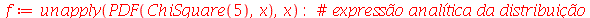 |
Vamos conferir o resultado para a media usando a definição.
| > |
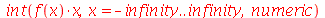 |
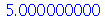 |
(2.7.2) |
Vamos conferir o resultado para a moda.
| > |
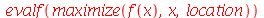 |
![.1541803298, {[{x = 3.}, .1541803298]}](images/curso9_264.gif) |
(2.7.3) |
Note que o máximo ocorre no ponto 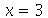 , que é a moda. Vamos conferir o resultado da mediana.
, que é a moda. Vamos conferir o resultado da mediana.
| > |
 |
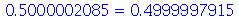 |
(2.7.4) |
| > |
|
Desvio Padrão, Variância, Assimetria e Curtose
Se 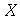 é uma variável aleatória em um espaço amostral discreto constituído pelo conjunto de pontos
é uma variável aleatória em um espaço amostral discreto constituído pelo conjunto de pontos ![a[1] .. a[n]](images/curso9_269.gif) (sem repetições,
(sem repetições, 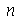 podendo ser infinito) com média
podendo ser infinito) com média 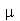 , a variância
, a variância 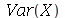 (
Variance
) é definida como
(
Variance
) é definida como
![Var(X) = sum(`*`(P(X = a[i]), `*`(`^`(`+`(a[i], `-`(mu)), 2))), i = 1 .. n)](images/curso9_273.gif)
onde ![P(X = a[i])](images/curso9_274.gif) é a probabilidade da variável
é a probabilidade da variável 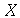 ter o valor
ter o valor ![a[i]](images/curso9_276.gif) . Se o espaço amostral é a reta real, a média é definida como
. Se o espaço amostral é a reta real, a média é definida como
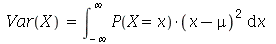
Uma forma alternativa de definir variância é como a média 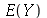 de uma nova variável aleatória
de uma nova variável aleatória 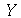 definida como
definida como 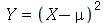 , isto é,
, isto é,
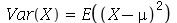
Por exemplo, vamos checar que esta segunda definição usando uma variável aleatória 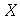 com a distribuição de probabilidades
ChiSquare
de 5 graus de liberdade:
com a distribuição de probabilidades
ChiSquare
de 5 graus de liberdade:
| > |
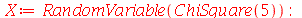 |
| > |
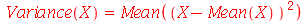 |
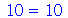 |
(2.8.1) |
| > |
|
O comando
Variance
quando aplicado em uma amostra ou lista de dados ![A[1], () .. (), A[n]](images/curso9_286.gif) calcula a variância usando estimativa imparcial ou não-viciada (unbiased estimation of variance), cuja fórmula é
calcula a variância usando estimativa imparcial ou não-viciada (unbiased estimation of variance), cuja fórmula é
![`/`(`*`(sum(`*`(`^`(`+`(A[i], `-`(conjugate(A))), 2)), i = 1 .. n)), `*`(`+`(n, `-`(1))))](images/curso9_287.gif)
O desvio padrão 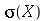 (
StandardDeviation
) é definido como
(
StandardDeviation
) é definido como
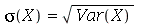
O desvio padrão é uma medida do tamanho da dispersão do pontos de uma amostra em torno da média. Se a dispersão for pequena, o desvio padrão é pequeno e vice-versa. O comando
StandardDeviation
quando aplicado em uma amostra ou lista de dados usa a estimativa imparcial. Para encontrar a estimativa parcial, devemos multiplicar o resultado por 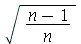 .
.
Exercícios
1. Considere o gráfico de uma distribuição Normal de média 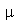 e desvio padrão
e desvio padrão 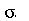 Mostre que a distância horizontal do ponto médio do gráfico até o ponto de inflexão (ponto onde a derivada segunda se anula) é
Mostre que a distância horizontal do ponto médio do gráfico até o ponto de inflexão (ponto onde a derivada segunda se anula) é 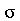 .
.
2. É possível mostrar de maneira geral que
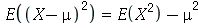
Verifique no Maple que este fato é verdeiro para a uma variável 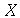 com uma distribuição Normal de média
com uma distribuição Normal de média 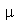 e desvio padrão
e desvio padrão 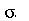
A assimetria (
Skewness
) é definida como
 = `/`(`*`(E(`*`(`^`(`+`(X, `-`(mu)), 3)))), `*`(`^`(sigma, 3)))](images/curso9_298.gif)
A assimetria ![alpha[3]](images/curso9_299.gif) é uma medida da assimetria de uma distribuição de probabilidades:
é uma medida da assimetria de uma distribuição de probabilidades: ![alpha[3]](images/curso9_300.gif) é positiva se for a distribuição de probabilidades for assimétrica à direita (veja o gráfico de
é positiva se for a distribuição de probabilidades for assimétrica à direita (veja o gráfico de 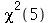 ), caso contrário
), caso contrário ![alpha[3]](images/curso9_302.gif) é negativa. Por exemplo, a distribuição
é negativa. Por exemplo, a distribuição 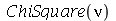 de
de 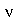 graus de liberdade é assimétrica à equerda para qualquer valor de
graus de liberdade é assimétrica à equerda para qualquer valor de 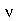 . Note que a assimetria
. Note que a assimetria ![alpha[3]](images/curso9_306.gif) é positiva.
é positiva.
| > |
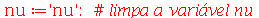 |
| > |
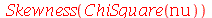 |
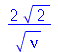 |
(2.8.2) |
A distribuição Beta com o segundo parâmetro menor do que o primeiro é um exemplo de assimetria negativa
| > |
 |
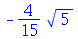 |
(2.8.3) |
Note que o gráfico é assimétrico à esquerda:
| > |
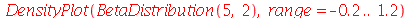 |
A curtose (
Kurtosis
) é definida como
 = `/`(`*`(E(`*`(`^`(`+`(X, `-`(mu)), 4)))), `*`(`^`(sigma, 4)))](images/curso9_314.gif)
A curtose mede o grau de agudez do pico da distribuição de probabilidades tomando a distribuição Normal como referência. A curtose da distribuição Normal é 3. Se a curtose for maior do que 3, a distribuição é mais concentrada em torno da média do que a distribuição Normal e se for menor do que 3, a distribuiçãoé mais espalhada do que a distribuição Normal. Note que
| > |
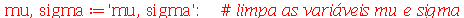 |
| > |
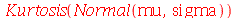 |
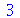 |
(2.8.4) |
O menor valor possível da curtose é 1 que é obtida com a distribuição de probabilidades discreta de
Bernoulli
quando a probabilidade de sucesso é 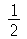 .
.
| > |
 |
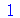 |
(2.8.5) |
| > |
|
Exercício
Moste usando Maple que a curtose da distribuição 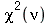 é sempre maior do que a curtose da distribuição normal.
é sempre maior do que a curtose da distribuição normal.
Percentil, Intervalo Interquartílico e Desvio Médio
Considere uma distribuição de probabilidades contínua, por exemplo, a distribuição normal de média 0 e desvio padrão 1. Qual é o valor de 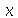 tal que a probabilidade de se obter um valor menor ou igual a
tal que a probabilidade de se obter um valor menor ou igual a 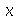 seja de 30%? A resposta seria o valor de
seja de 30%? A resposta seria o valor de 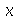 tal que a integral de
tal que a integral de 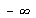 a
a 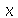 dê
dê 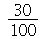 . A interpretação geométrica é a área embaixo da curva da distribuição de probabilidades de
. A interpretação geométrica é a área embaixo da curva da distribuição de probabilidades de 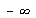 a
a 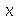 é
é 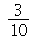 . Este valor de
. Este valor de 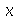 é chamado de trigésimo percentil. Para calcular um percentil, devemos usar o comando
Percentile
, no caso do trigésimo percentil, o comando é
é chamado de trigésimo percentil. Para calcular um percentil, devemos usar o comando
Percentile
, no caso do trigésimo percentil, o comando é
| > |
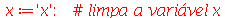 |
| > |
![x[30] := Percentile(Normal(0, 1), 30, numeric); 1](images/curso9_333.gif) |
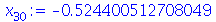 |
(2.9.1) |
Vamos verificar o resultado
| > |
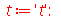 |
| > |
![int(PDF(Normal(0, 1), t), t = `+`(`-`(infinity)) .. x[30])](images/curso9_336.gif) |
| > |
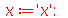 |
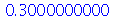 |
(2.9.2) |
Este valor de 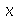 também é chamado de terceiro decil, e também pode ser calculado com o comando
Decile
:
também é chamado de terceiro decil, e também pode ser calculado com o comando
Decile
:
| > |
 |
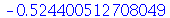 |
(2.9.3) |
O intervalo interquartílico (
InterquartileRange
) é definido como a diferença entre o septagésimo-quinto (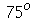 ) percentil e o vigésimo-quinto (
) percentil e o vigésimo-quinto (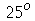 ) percentil ou, equivalentemente, a diferença entre o terceiro quartil e o primeiro quartil (
Quartile
). Por exemplo, no caso da distribuição normal
) percentil ou, equivalentemente, a diferença entre o terceiro quartil e o primeiro quartil (
Quartile
). Por exemplo, no caso da distribuição normal
| > |
 |
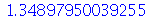 |
(2.9.4) |
Só para confirmar:
| > |
 |
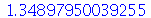 |
(2.9.5) |
| > |
 |
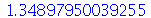 |
(2.9.6) |
O intervalo semi-interquartílico é definido como a metade do intervalo interquartílico.
O desvio médio é definido como média 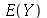 de uma nova variável aleatória
de uma nova variável aleatória 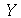 definida como
definida como 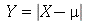 , isto é,
, isto é,
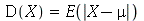
| > |
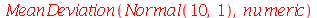 |
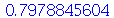 |
(2.9.7) |
Podemos confirmar com os seguintes comandos:
| > |
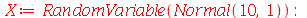 |
| > |
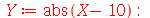 |
| > |
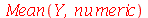 |
 |
(2.9.8) |
O desvio mediano absoluto é definido como médiana de uma nova variável aleatória 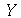 definida como
definida como 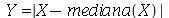 , isto é,
, isto é,
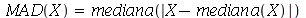
Por exemplo:
| > |
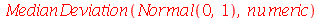 |
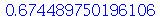 |
(2.9.9) |
Podemos confirmar com os seguintes comandos:
| > |
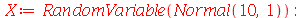 |
| > |
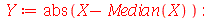 |
| > |
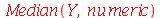 |
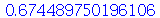 |
(2.9.10) |
| > |
|
Função Geradora de Momentos e Função Característica
A partir de uma variável aleatória 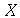 podemos definir uma nova variável aleatória
podemos definir uma nova variável aleatória 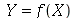 usando uma função
usando uma função 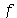 . Podemos usar
. Podemos usar 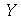 em os comandos que tem variáveis aleatórias como argumento, como o comando que calcula a média ou o desvio padrão. Em particular, se a função for
em os comandos que tem variáveis aleatórias como argumento, como o comando que calcula a média ou o desvio padrão. Em particular, se a função for 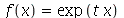 , teremos a nova variável aleatória
, teremos a nova variável aleatória 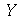 defina como
defina como 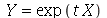 . A função geradora de momentos (
MomentGeneratingFunction
) é definida como a média de
. A função geradora de momentos (
MomentGeneratingFunction
) é definida como a média de 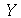 , isto é,
, isto é,
 = E(exp(`*`(t, `*`(X))))](images/curso9_377.gif)
O 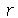 -ésimo momento (
Moment
) de uma variável aleatória
-ésimo momento (
Moment
) de uma variável aleatória 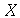 e definido por
e definido por
![(diff(mu(x), x))[r] = E(`^`(X, r))](images/curso9_380.gif)
e o 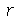 -ésimo momento central (
CentralMoment
) de uma variável aleatória
-ésimo momento central (
CentralMoment
) de uma variável aleatória 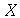 e definido como a média da variável aleatória
e definido como a média da variável aleatória 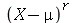 , onde
, onde 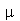 é a média de
é a média de 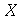 , isto é, por
, isto é, por
![mu[r] = E(`^`(`+`(X, `-`(mu)), r))](images/curso9_386.gif)
Por exemplo
| > |
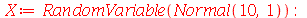 |
| > |
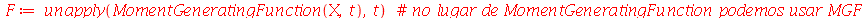 |
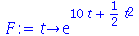 |
(2.10.1) |
Note que se expandirmos a função geradora de momentos em série de Taylor
| > |
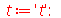 |
| > |
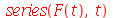 |
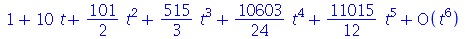 |
(2.10.2) |
podemos obter o 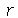 -ésimo momento como o coeficiente do termo
-ésimo momento como o coeficiente do termo 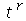 vezes o fatorial de
vezes o fatorial de 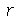 . De fato
. De fato
| > |
 |
| > |
![seq(mu[r] = `/`(`*`(Mean(`^`(X, r))), `*`(factorial(r))), r = 0 .. 5)](images/curso9_397.gif) |
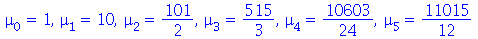 |
(2.10.3) |
De outra maneira
| > |
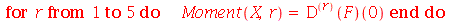 |
| > |
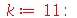 |
| > |
 |
| > |
![X[i] := RandomVariable(EmpiricalDistribution([1, -1], probabilities = [`/`(1, 2), `/`(1, 2)])); -1](images/curso9_407.gif) |
| > |
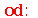 |
| > |
![expand(convert(MomentGeneratingFunction(add(X[i], i = 1 .. k), omega), trig))](images/curso9_409.gif) |
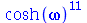 |
(2.10.5) |
| > |
|
Exercício
Seja ![X[i]](images/curso9_411.gif) para
para 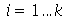 variáveis aleatórias independentes que podem assumir os valores 1 ou -1 com probabilidade uniforme. Escolha
variáveis aleatórias independentes que podem assumir os valores 1 ou -1 com probabilidade uniforme. Escolha 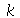 como sendo um número inteiro maior do que 10. (a) Mostre que a função geradora de momentos variável aleatória
como sendo um número inteiro maior do que 10. (a) Mostre que a função geradora de momentos variável aleatória 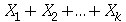 é
é 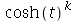 . (b) Mostre que a função geradora de momentos da variável aleatória
. (b) Mostre que a função geradora de momentos da variável aleatória 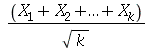 é
é 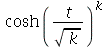 .
.
Solução
(a) Vamos mostrar no caso em que 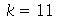 :
:
| > |
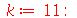 |
| > |
 |
| > |
![X[i] := RandomVariable(EmpiricalDistribution([1, -1], probabilities = [`/`(1, 2), `/`(1, 2)])); -1](images/curso9_421.gif) |
| > |
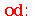 |
| > |
![expand(convert(MGF(add(X[i], i = 1 .. k), t), trig))](images/curso9_423.gif) |
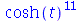 |
(2.10.1.1.1) |
(b)
| > |
![res := expand(convert(MGF(`/`(`*`(add(X[i], i = 1 .. k)), `*`(sqrt(k))), t), trig)); -1](images/curso9_425.gif) |
| > |
 |
| > |
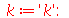 |
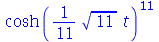 |
(2.10.1.1.2) |
A função característica (
CharacteristicFunction
) é definida como a média de 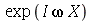 , isto é,
, isto é,
 = E(exp(`*`(I, `*`(omega, `*`(X)))))](images/curso9_430.gif)
Por exemplo
| > |
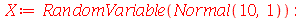 |
| > |
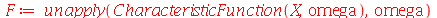 |
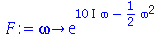 |
(2.10.6) |
Note que se expandirmos a função característica em série de Taylor
| > |
 |
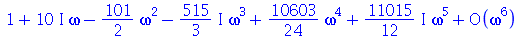 |
(2.10.7) |
podemos obter o 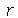 -ésimo momento como o coeficiente do termo
-ésimo momento como o coeficiente do termo 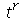 vezes
vezes 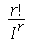 . De fato
. De fato
| > |
![seq(mu[r] = `/`(`*`(Mean(`^`(`*`(I, `*`(X)), r))), `*`(factorial(r))), r = 0 .. 5)](images/curso9_439.gif) |
![mu[0] = 1, mu[1] = `*`(10, `*`(I)), mu[2] = -`/`(101, 2), mu[3] = `+`(`-`(`*`(`/`(515, 3), `*`(I)))), mu[4] = `/`(10603, 24), mu[5] = `*`(`/`(11015, 12), `*`(I))](images/curso9_440.gif) |
(2.10.8) |
De outra maneira
| > |
 |
| > |
|
Exercício
Seja ![X[i]](images/curso9_447.gif) para
para 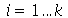 variáveis aleatórias independentes que podem assumir os valores 1 ou -1 com probabilidade uniforme. Escolha
variáveis aleatórias independentes que podem assumir os valores 1 ou -1 com probabilidade uniforme. Escolha 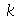 como sendo um número inteiro maior do que 10. (a) Mostre que a função característica da variável aleatória
como sendo um número inteiro maior do que 10. (a) Mostre que a função característica da variável aleatória 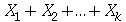 é
é 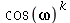 . (b) Mostre que a função característica da variável aleatória
. (b) Mostre que a função característica da variável aleatória 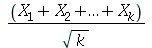 é
é 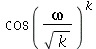 .
.
Estatística
Amostragem
Na Estatística, usualmente temos uma população de indivíduos (por exemplo: pessoas, produtos, ou objetos) e queremos tirar conclusões sobre as características desta população examinando um subgrupo que é chamado de amostra. Quando selecionamos uma amostra, vamos supor que cada indivíduo é selecionado aleatoriamente segundo uma distribuição de probabilidades associada à população. O tamanho da população pode ser grande, ou até mesmo infinito, mas o tamanho da amostra deve ser o menor possível por uma questão de economia de recursos. A amostragem pode ser com ou sem reposição, dependendo se um indivíduo selecionado foi colocado de volta na população ou não. No primeiro caso, amostra com reposição, um indivíduo pode ser selecionado mais do que uma vez. Os parâmetros da população são os parâmetros da distribuição de probabilidades associada. Por exemplo, uma população associada a distribuição normal (chamada população normal) tem como parâmetros a média 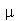 e o desvio padrão
e o desvio padrão 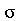 da distribuição normal. O objetivo da Estatística é usar dados amostrais para obter valores numéricos que sirvam para estimar e testar hipóteses sobre os parâmetros da população. Os valores numéricos são aproximações dos parâmetros da população e estimativas de erros são bem-vindos.
da distribuição normal. O objetivo da Estatística é usar dados amostrais para obter valores numéricos que sirvam para estimar e testar hipóteses sobre os parâmetros da população. Os valores numéricos são aproximações dos parâmetros da população e estimativas de erros são bem-vindos.
Se fizermos várias amostragens, podemos definir novas variáveis aleatórias que terão suas próprias distribuições de probabilidades. Por exemplo, vamos supor que uma amostra ![X[1], () .. (), X[n]](images/curso9_456.gif) tem tamanho
tem tamanho 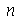 . Vamos definir uma nova variável aleatória
. Vamos definir uma nova variável aleatória
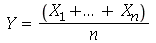
chamada média amostral. Podemos agora nos perguntar qual é a distribuição de probabilidades associada à 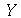 uma vez conhecida a distribuição de probabilidades associada à
uma vez conhecida a distribuição de probabilidades associada à 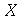 . Teremos um valor de
. Teremos um valor de 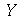 cada vez que uma amostragem de tamanho
cada vez que uma amostragem de tamanho 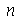 for realizada. Usuamente a variável
for realizada. Usuamente a variável 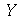 é denotada por
é denotada por 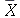 .
.
Exemplo 1. A altura da população brasileira obedeçe aproximadamente uma distribuição normal de média 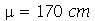 e desvio padrão
e desvio padrão 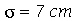 . Suponha que selecionamos amostras cada uma com 30 indivíduos. (a) Qual é a média e o desvio padrão da média amostral? (b) Suponha que selecionamos 50 amostras. Em quantas amostras encontramos a média entre
. Suponha que selecionamos amostras cada uma com 30 indivíduos. (a) Qual é a média e o desvio padrão da média amostral? (b) Suponha que selecionamos 50 amostras. Em quantas amostras encontramos a média entre 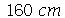 e
e 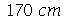 .
.
Solução. Antes de resolvermos este problema, note que podemos fazer uma simulação no Maple de um experimento deste tipo com a população brasileira.
| > |
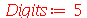 |
| > |
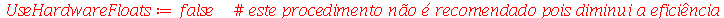 |
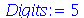 |
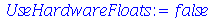 |
(3.1.1) |
| > |
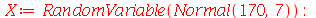 |
| > |
![for i from 0 to 50 do amostra[i] := Sample(X, 30) end do; -1](images/curso9_474.gif) |
| > |
![L := [seq(Mean(amostra[i]), i = 1 .. 50)]](images/curso9_475.gif) |
| > |
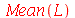 |
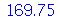 |
(3.1.3) |
| > |
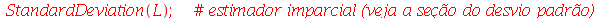 |
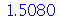 |
(3.1.4) |
| > |
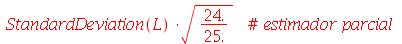 |
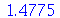 |
(3.1.5) |
Podemos ver que a média amostral deu muito próximo da média 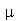 porém o desvio padrão das médias amostrais deu bem diferente de
porém o desvio padrão das médias amostrais deu bem diferente de 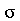 . Os resultados corretos do item (a) podem ser obtidos da seguinte forma:
. Os resultados corretos do item (a) podem ser obtidos da seguinte forma:
| > |
![for i to 30 do X[i] := RandomVariable(Normal(170, 7)) end do; -1](images/curso9_488.gif) |
| > |
![Y := `+`(`*`(`/`(1, 30), `*`(add(X[i], i = 1 .. 30)))); -1](images/curso9_489.gif) |
| > |
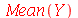 |
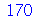 |
(3.1.6) |
| > |
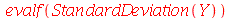 |
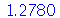 |
(3.1.7) |
Pela teoria da Estatística, quando a população é infinita ou quando a amostragem é com reposição, o desvio padrão é dado por
![sigma[conjugate(X)] = `/`(`*`(sigma), `*`(sqrt(n)))](images/curso9_494.gif)
No exemplo acima, temos ![`and`(sigma[conjugate(X)] = `+`(`/`(`*`(7), `*`(sqrt(30)))), `+`(`/`(`*`(7), `*`(sqrt(30)))) = 1.2781)](images/curso9_495.gif) . Portanto, se fizermos um experimento com a população brasileira selecionando 50 amostras aleatórias de 30 indivíduos, após calcularmos
. Portanto, se fizermos um experimento com a população brasileira selecionando 50 amostras aleatórias de 30 indivíduos, após calcularmos ![sigma[conjugate(X)]](images/curso9_496.gif) , podemos estimar o desvio padrão da população brasileira multiplicando o valor de
, podemos estimar o desvio padrão da população brasileira multiplicando o valor de ![sigma[conjugate(X)]](images/curso9_497.gif) dado pela Eq.
dado pela Eq. 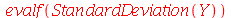 por
por 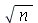 =5.4772.
=5.4772.
O ítem (b) pede quantas amostras encontramos a média entre 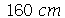 e
e 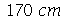 . Na simulação feita acima, o número de amostras é
. Na simulação feita acima, o número de amostras é
| > |
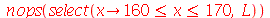 |
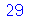 |
(3.1.8) |
No entanto, o resultado correto é encontrado calculando a área embaixo da curva da distribuição de probabilidades de 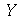 no intervalo
no intervalo ![[160, 170]](images/curso9_505.gif) . Isto é calculado da seguinte forma:
. Isto é calculado da seguinte forma:
| > |
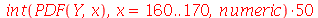 |
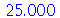 |
(3.1.9) |
| > |
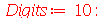 |
| > |
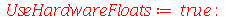 |
| > |
|
Um teorema importante da Estatística afirma que a variável aleatória padronizada ![Z = `/`(`*`(`+`(conjugate(X), `-`(mu[conjugate(X)]))), `*`(sigma[conjugate(X)]))](images/curso9_510.gif) é assintoticamente normal com média 0 e desvio padrão 1. Na prática, se o tamanho da amostra for
é assintoticamente normal com média 0 e desvio padrão 1. Na prática, se o tamanho da amostra for 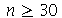 , o teorema pode ser aplicado com alguma margem de segurança.
, o teorema pode ser aplicado com alguma margem de segurança.
Exemplo 2. Uma máquina produz peças que pesam na média 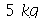 com um desvio padrão de
com um desvio padrão de 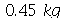 . Um lote de 50 peças deve ser transportado. (a) Qual é a probabilidade do peso total estar entre 245 e 255
. Um lote de 50 peças deve ser transportado. (a) Qual é a probabilidade do peso total estar entre 245 e 255 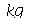 ? (b) Qual é a probabilidade do peso total ser maior do que 255
? (b) Qual é a probabilidade do peso total ser maior do que 255 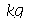 ?
?
Solução. Vamos usar a distribuição normal com média 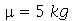 e desvio padrão
e desvio padrão 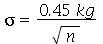 onde
onde 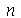 é o tamanho da amostra. A solução do ítem (a) é
é o tamanho da amostra. A solução do ítem (a) é
| > |
 |
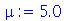 |
(3.1.10) |
| > |
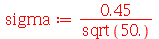 |
 |
(3.1.11) |
| > |
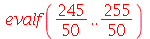 |
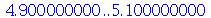 |
(3.1.12) |
| > |
 |
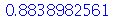 |
(3.1.13) |
e do ítem (b) é
| > |
 |
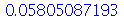 |
(3.1.14) |
| > |
|
Exercício
O peso médio dos produtos de uma loja de departamentos é de 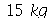 e desvio padrão
e desvio padrão 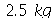 . Qual é a propabilidade de que 200 pacotes escolhidos aleatoriamente ultrapasse o peso limite do elevador, que é
. Qual é a propabilidade de que 200 pacotes escolhidos aleatoriamente ultrapasse o peso limite do elevador, que é 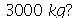
Suponha novamente que ![X[1], () .. (), X[n]](images/curso9_532.gif) são variáveis aleatórias independentes associadas a mesma distribuição de probabilidades com média
são variáveis aleatórias independentes associadas a mesma distribuição de probabilidades com média 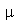 e desvio padrão
e desvio padrão 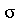 . A variância amostral
. A variância amostral 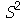 é definida como
é definida como
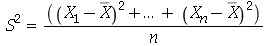
Pode-se mostrar que 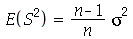 . Uma vez que
. Uma vez que 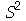 é um estimador parcial da variância, definimos um novo estimador imparcial ou não-viciado
é um estimador parcial da variância, definimos um novo estimador imparcial ou não-viciado
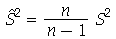
que tem a propriedade 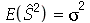 . Portanto,
. Portanto, 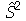 é um estimador imparcial da variância. Note que os comandos
Variance
e
StandardDeviation
, quando aplicados em uma amostra, lista de dados ou matriz de dados, usam o estimamor imparcial para o cálculo da variância amostral e do desvio padrão amostral.
é um estimador imparcial da variância. Note que os comandos
Variance
e
StandardDeviation
, quando aplicados em uma amostra, lista de dados ou matriz de dados, usam o estimamor imparcial para o cálculo da variância amostral e do desvio padrão amostral.
Vamos verificar através de uma simulação para um valor pequeno de 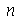 que a média de
que a média de 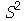 é
é 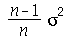 .
.
| > |
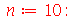 |
| > |
![for i to n do X[i] := RandomVariable(ChiSquare(11)) end do; -1](images/curso9_546.gif) |
| > |
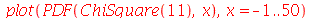 |
 |
|
| > |
![Xbarra := `/`(`*`(add(X[i], i = 1 .. n)), `*`(n)); -1](images/curso9_549.gif) |
| > |
![S2 := `/`(`*`(add(`*`(`^`(`+`(X[i], `-`(Xbarra)), 2)), i = 1 .. n)), `*`(n)); -1](images/curso9_550.gif) |
| > |
![Mean(S2) = `/`(`*`(`+`(n, `-`(1)), `*`(`^`(StandardDeviation(X[2]), 2))), `*`(n))](images/curso9_551.gif) |
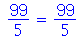 |
(3.1.15) |
| > |
|
Para facilitar o cálculo da distribuição de probabilidades, um terceiro estimador é definido como
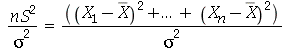
A distribuição de probabilidades de 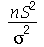 é
é 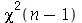 , isto é, Chi-quadrado com
, isto é, Chi-quadrado com 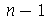 graus de liberdade, se as variáveis originais forem normais. Podemos verificar por simulações que a distribuição de probabilidades de
graus de liberdade, se as variáveis originais forem normais. Podemos verificar por simulações que a distribuição de probabilidades de 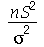 é
é 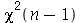 tomando valores específicos para
tomando valores específicos para 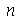 e definindo variáveis aleatórias normais. Por exemplo:
e definindo variáveis aleatórias normais. Por exemplo:
| > |
 |
| > |
 |
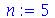 |
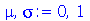 |
(3.1.16) |
| > |
![for i to n do X[i] := RandomVariable(Normal(mu, sigma)) end do; -1](images/curso9_564.gif) |
| > |
![Xbarra := `/`(`*`(add(X[i], i = 1 .. n)), `*`(n)); -1](images/curso9_565.gif) |
| > |
![nSsigma := `/`(`*`(add(`*`(`^`(`+`(X[i], `-`(Xbarra)), 2)), i = 1 .. n)), `*`(`^`(sigma, 2))); -1](images/curso9_566.gif) |
| > |
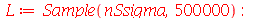 |
| > |
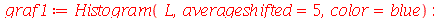 |
| > |
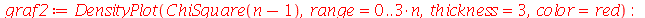 |
| > |
![display([graf1, graf2])](images/curso9_570.gif) |
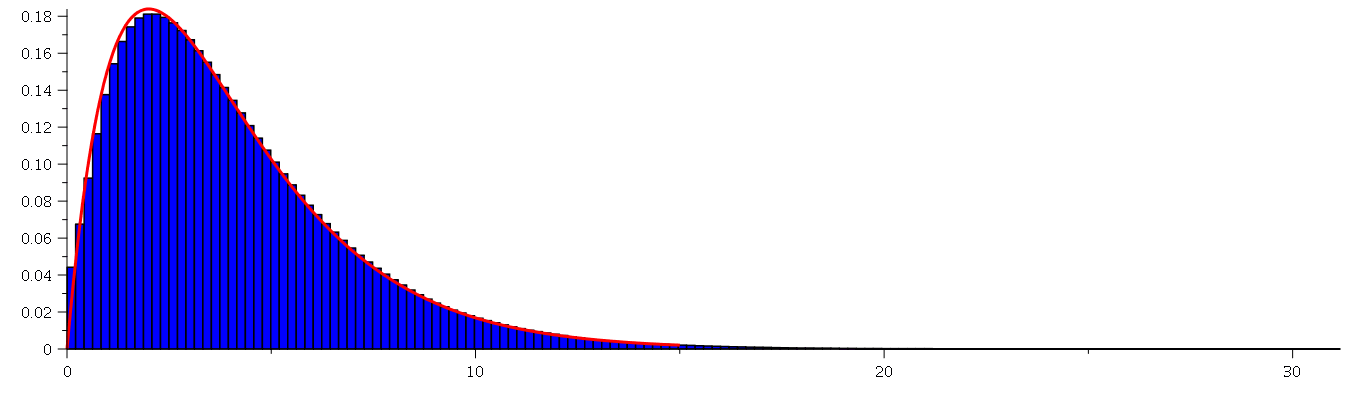 |
|
| > |
|
Note que a curva vermelha, que é a distribuição de probabilidades de 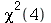 , é muito bem aproximada pelo histograma (
histogram
) de uma amostra com 50000 valores. Podemos testar facilmente para outros valores de
, é muito bem aproximada pelo histograma (
histogram
) de uma amostra com 50000 valores. Podemos testar facilmente para outros valores de 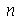 .
.
Exemplo 3. Vimos no Exemplo 1 que a altura da população brasileira obedeçe aproximadamente uma distribuição normal de média 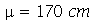 e desvio padrão
e desvio padrão 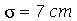 . Qual é o desvio padrão das variâncias usando o estimador imparcial para amostras de tamanho
. Qual é o desvio padrão das variâncias usando o estimador imparcial para amostras de tamanho 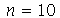 , isto é,
, isto é, ![sigma[`*`(`^`(\, 2))]](images/curso9_577.gif) ?
?
Solução.
| > |
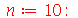 |
| > |
![for i to n do X[i] := RandomVariable(Normal(170, 7)) end do; -1](images/curso9_579.gif) |
| > |
![Xbarra := `/`(`*`(add(X[i], i = 1 .. n)), `*`(n)); -1](images/curso9_580.gif) |
| > |
![Schapeu2 := `/`(`*`(add(`*`(`^`(`+`(X[i], `-`(Xbarra)), 2)), i = 1 .. n)), `*`(`+`(n, `-`(1)))); -1](images/curso9_581.gif) |
| > |
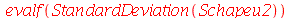 |
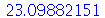 |
(3.1.17) |
Exemplo 4. O desvio padrão dos pesos de uma população de uma cidade é 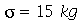 . Suponha que 200 pessoas são selecionadas aleatoriamente e o desvio padrão é calculado. Este processo é repetido diversas vezes. (a) Calcule a média da distribuição de desvios padrões. (b) Calcule o desvio padrão da distribuição de desvios padrões.
. Suponha que 200 pessoas são selecionadas aleatoriamente e o desvio padrão é calculado. Este processo é repetido diversas vezes. (a) Calcule a média da distribuição de desvios padrões. (b) Calcule o desvio padrão da distribuição de desvios padrões.
Solução. Vamos supor que a distribuição de probabilidades dos pesos da população desta cidade é normal. Portanto, A distribuição de probabilidades de 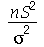 é
é 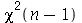 . A variável aleatória
. A variável aleatória 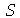 é dada por
é dada por 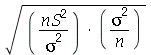 . As respostas são encontradas calculando a média e o desvio padrão de
. As respostas são encontradas calculando a média e o desvio padrão de 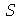 .
.
(a)
| > |
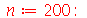 |
| > |
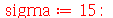 |
| > |
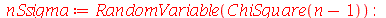 |
| > |
 |
| > |
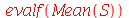 |
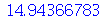 |
(3.1.18) |
(b)
| > |
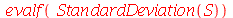 |
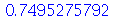 |
(3.1.19) |
Para amostras grandes (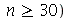 , o desvio padrão de
, o desvio padrão de 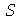 pode ser calculado através da fórmula
pode ser calculado através da fórmula ![sigma[S] = `/`(`*`(sigma), `*`(sqrt(`+`(`*`(2, `*`(n))))))](images/curso9_600.gif) .
.
| > |
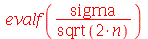 |
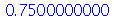 |
(3.1.20) |
| > |
|
M. Spiegel, Probabilidade e Estatística, 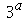 edição
edição
Cap 5, problemas 5.128 e 5.130.
Estimação e intervalo de confiança
Uma estatística é um estimador imparcial ou não viciado de um parâmetro se sua média é igual ao parâmetro correspondente na população. Se duas estimativas tem a mesma média, o estimador mais eficiente é aquele que tem o menor desvio padrão. Podemos ter estimativa por ponto, quando apenas um número é usado, ou estimativa por intervalo, quando mais de um número é usado. A confiança é a previsão de erro ou a precisão de uma estimativa.
Suponha que uma estatística 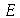 tem média
tem média ![mu[E]](images/curso9_605.gif) e desvio padrão
e desvio padrão ![sigma[E]](images/curso9_606.gif) . Se a distribuição amostral de
. Se a distribuição amostral de 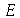 for aproximadamente normal, o valor de
for aproximadamente normal, o valor de 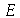 será encontrado no intervalo
será encontrado no intervalo
![`+`(mu[E], `&+-`(`*`(z, `*`(sigma[E]))))](images/curso9_609.gif)
com a probabilidade ![P(`and`(`<=`(`+`(`-`(`*`(z, `*`(sigma[E]))), mu[E]), E), `<=`(E, `+`(`*`(z, `*`(sigma[E])), mu[E]))))](images/curso9_610.gif) , que é chamada de nível de confiança. O parâmetro
, que é chamada de nível de confiança. O parâmetro 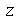 é chamado valor crítico. Por exemplo, para uma distribuição normal (qualquer que seja a média e o desvio padrão), o nível de confiança é aproximadamente 95.45% quando o valor crítico é
é chamado valor crítico. Por exemplo, para uma distribuição normal (qualquer que seja a média e o desvio padrão), o nível de confiança é aproximadamente 95.45% quando o valor crítico é 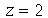 .
.
| > |
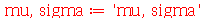 |
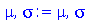 |
(3.2.1) |
| > |
 |
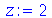 |
(3.2.2) |
| > |
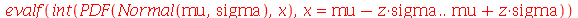 |
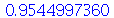 |
(3.2.3) |
A área correspondente sob a curva da distribuição normal na variável padronizada é área azul do gráfico a seguir.
| > |
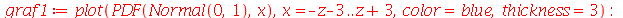 |
| > |
 |
| > |
![display([graf1, graf2])](images/curso9_621.gif) |
Usualmente o sub-índice de 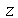 denota a probabilidade acumulada até o valor
denota a probabilidade acumulada até o valor 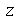 . No caso acima, temos
. No caso acima, temos
| > |
, 2))](images/curso9_625.gif) |
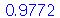 |
(3.2.4) |
Assim, denotamos ![z[.9772] = 2](images/curso9_627.gif) . O valor de
. O valor de 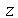 e do sub-índice para um nível de confiança de 95% é aproximadamente
e do sub-índice para um nível de confiança de 95% é aproximadamente ![z[.975] = 1.96](images/curso9_629.gif) e para um nível de confiança de 99% é aproximadamente
e para um nível de confiança de 99% é aproximadamente ![z[.995] = 2.58](images/curso9_630.gif) .
.
| > |
|
Intervalo de confiança para a média amostral para amostras grandes.
Para amostras grandes (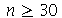 ), a média amostal
), a média amostal 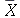 com um nível de confiança
com um nível de confiança 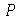 tem o intervalo de confiança
tem o intervalo de confiança 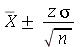 , onde
, onde 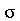 é o desvio padrão da população e
é o desvio padrão da população e 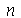 é o tamanho da amostra. Se o desvio padrão da população não é conhecido, usamos o intervalo
é o tamanho da amostra. Se o desvio padrão da população não é conhecido, usamos o intervalo 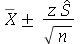 , onde
, onde 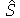 é o estimador imparcial do desvio padrão. O valor crítico
é o estimador imparcial do desvio padrão. O valor crítico 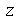 é calculado usando a distribuição normal, pois para
é calculado usando a distribuição normal, pois para 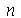 grande a variável aleatória padronizada
grande a variável aleatória padronizada ![Z = `/`(`*`(`+`(conjugate(X), `-`(mu[conjugate(X)]))), `*`(sigma[conjugate(X)]))](images/curso9_641.gif) é assintoticamente normal com média 0 e desvio padrão 1.
é assintoticamente normal com média 0 e desvio padrão 1.
Continuação do Exemplo 1. A altura da população brasileira obedeçe aproximadamente uma distribuição normal de média 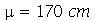 e desvio padrão
e desvio padrão 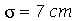 . Suponha que selecionamos 50 amostras cada uma com 30 indivíduos. (a) Qual é a média e o desvio padrão das 50 amostras? (b) Em quantas amostras encontramos a média entre
. Suponha que selecionamos 50 amostras cada uma com 30 indivíduos. (a) Qual é a média e o desvio padrão das 50 amostras? (b) Em quantas amostras encontramos a média entre 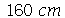 e
e 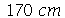 . (c) Qual é o intervalo para se ter 95% de confiança para estimar a altura média.
. (c) Qual é o intervalo para se ter 95% de confiança para estimar a altura média.
Solução. Os ítens (a) e (b) foram resolvidos na seção anterior. Vamos agora resolver o ítem (c). Quando o desvio padrão é conhecido, o intervalo de confiança é dado por 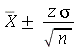 .
.
| > |
 |
 |
(3.2.5) |
Usamos o valor 0.975 pois devemos acrescentar a área de 2.5% aos 95% para poder usar a função de distribuição acumulada.
| > |
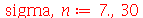 |
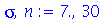 |
(3.2.6) |
| > |
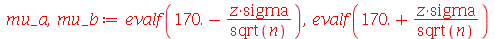 |
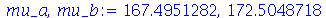 |
(3.2.7) |
| > |
 |
 |
(3.2.8) |
Uma maneira de fazer uma simulação para testar este intervalo é
| > |
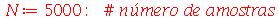 |
| > |
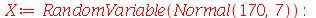 |
| > |
![for i to N do amostra[i] := Sample(X, n) end do; -1](images/curso9_657.gif) |
| > |
![L := [seq(Mean(amostra[i]), i = 1 .. N)]; -1](images/curso9_658.gif) |
| > |
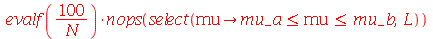 |
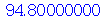 |
(3.2.9) |
| > |
|
Note que o resultado acima tem que dar próximo de 95%. Quanto maior for o número de amostras, mais perto de 95%.
Exercício
Calcule os valores críticos para um nível de confiança de 95% para a distribuição 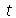 de Student.
de Student.
Intervalo de confiança para a média amostral para amostras pequenas.
Para amostras pequenas (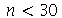 ), a média amostal
), a média amostal 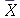 com um nível de confiança
com um nível de confiança 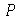 tem o intervalo de confiança
tem o intervalo de confiança 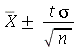 , onde
, onde 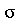 é o desvio padrão de população normal e
é o desvio padrão de população normal e 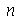 é o tamanho da amostra. Se o desvio padrão da população normal não é conhecido, usamos o intervalo
é o tamanho da amostra. Se o desvio padrão da população normal não é conhecido, usamos o intervalo 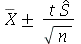 , onde
, onde 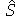 é o estimador imparcial do desvio padrão. O valor crítico
é o estimador imparcial do desvio padrão. O valor crítico 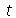 é calculado usando a distribuição t de Student
(StudentT
), pois para
é calculado usando a distribuição t de Student
(StudentT
), pois para 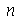 pequeno a variável aleatória padronizada
pequeno a variável aleatória padronizada ![Z = `/`(`*`(`+`(conjugate(X), `-`(mu[conjugate(X)])), `*`(sqrt(n))), `*`(\))](images/curso9_672.gif) obedece a distribuição t de Student. Portanto, para um nível de confiança de 95%, a variável
obedece a distribuição t de Student. Portanto, para um nível de confiança de 95%, a variável 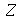 deve estar no invervalo
deve estar no invervalo ![`and`(`<`(`+`(`-`(t[.975])), Z), `<`(Z, t[.975]))](images/curso9_674.gif) , que produz o intervalo
, que produz o intervalo 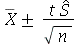 .
.
Vamos fazer uma simulação para checar que a variável aleatória padronizada ![Z = `/`(`*`(`+`(conjugate(X), `-`(mu[conjugate(X)])), `*`(sqrt(n))), `*`(\))](images/curso9_676.gif) obedece a distribuição t de Student e comparar com a distribuição normal. Vamos considerar amostras de tamanho
obedece a distribuição t de Student e comparar com a distribuição normal. Vamos considerar amostras de tamanho 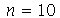 .
.
| > |
 |
| > |
![for i to n do X[i] := RandomVariable(Normal(mu, 1)) end do; -1](images/curso9_679.gif) |
| > |
![Xbarra := `/`(`*`(add(X[i], i = 1 .. n)), `*`(n)); -1](images/curso9_680.gif) |
| > |
![S2 := `/`(`*`(add(`*`(`^`(`+`(X[i], `-`(Xbarra)), 2)), i = 1 .. n)), `*`(`+`(n, `-`(1)))); -1](images/curso9_681.gif) |
| > |
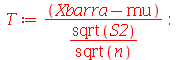 |
| > |
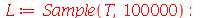 |
| > |
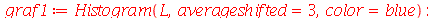 |
| > |
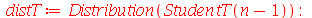 |
| > |
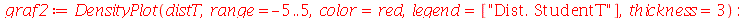 |
| > |

 |
| > |
![display([graf1, graf2, graf3])](images/curso9_689.gif) |
Para um nível de confiança de 95%, o valor de ![t[.975]](images/curso9_691.gif) é
é
| > |
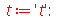 |
| > |
![t[.975] := fsolve(CDF(StudentT(9), x) = .975)](images/curso9_693.gif) |
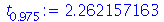 |
(3.2.10) |
que corresponde ao valor no eixo horizontal que delimita a área hachuriada no gráfico abaixo.