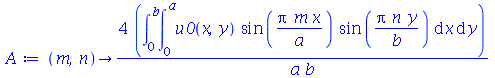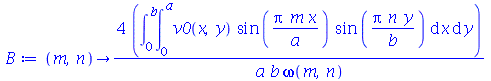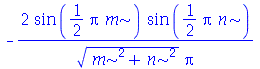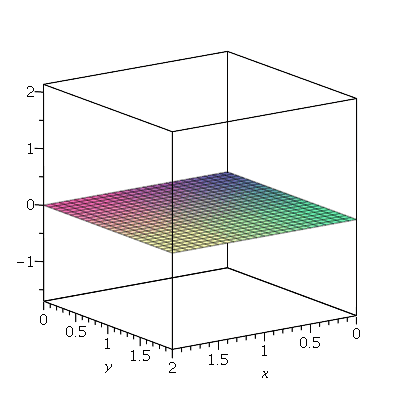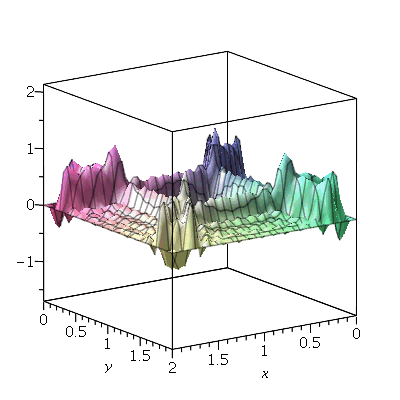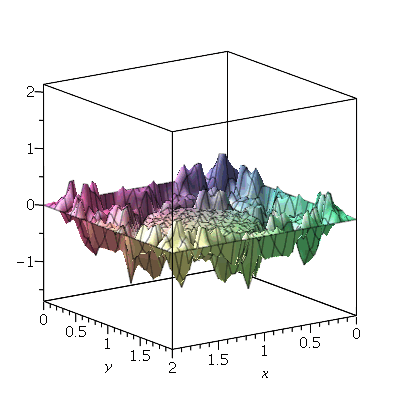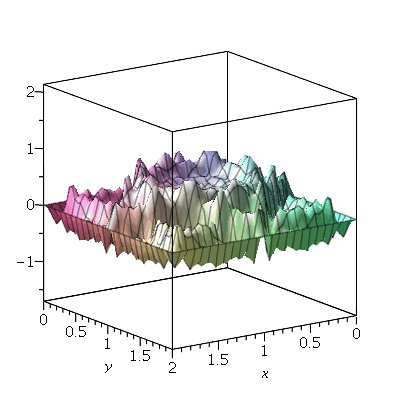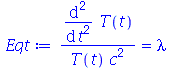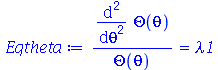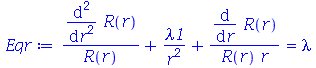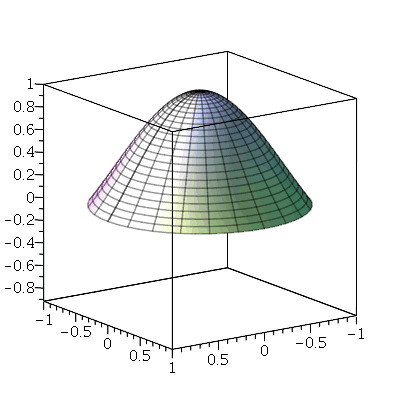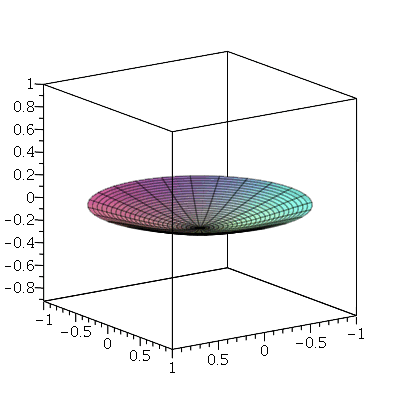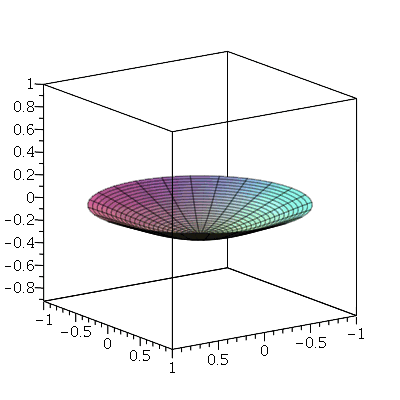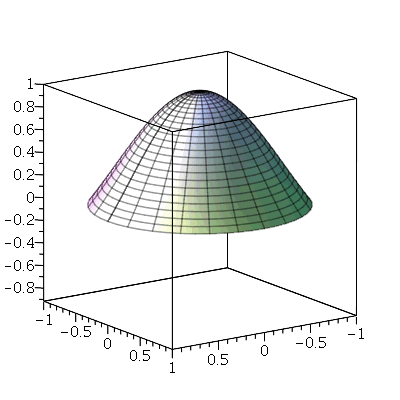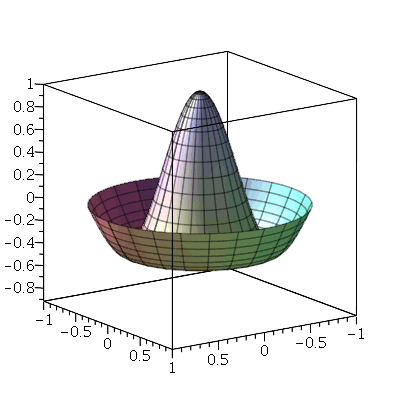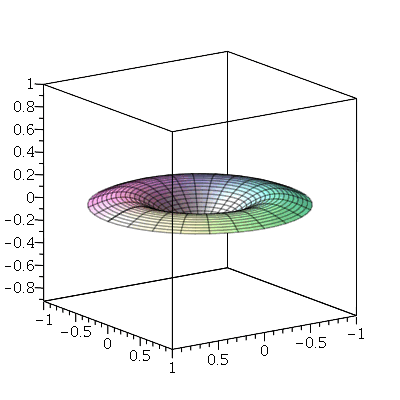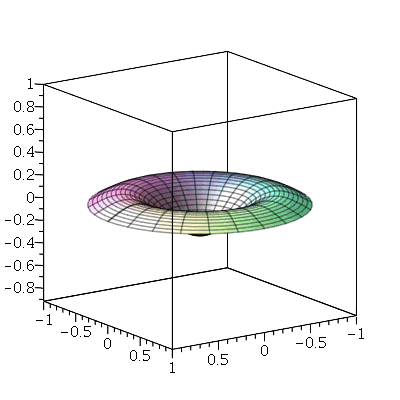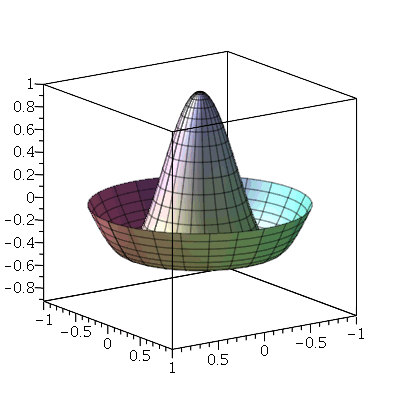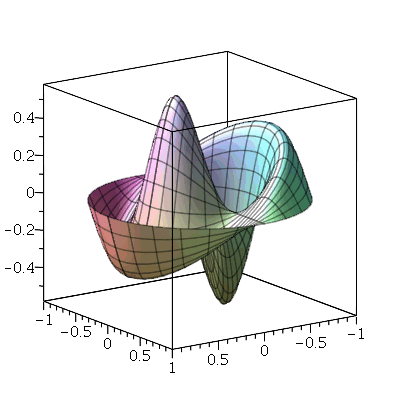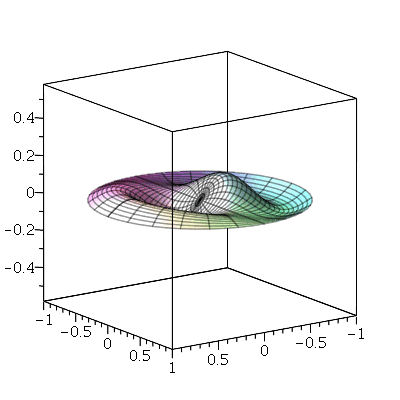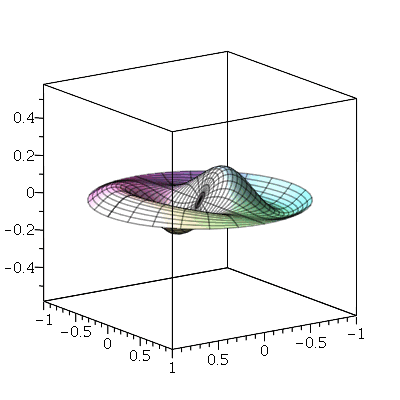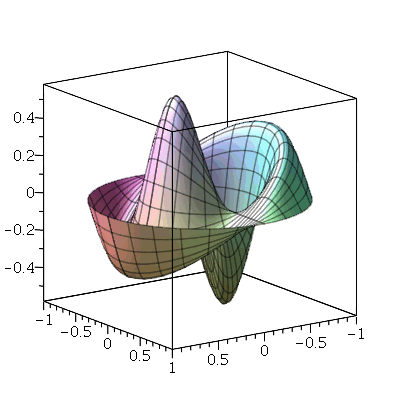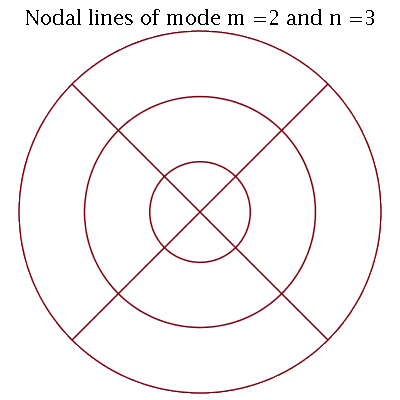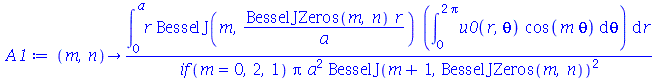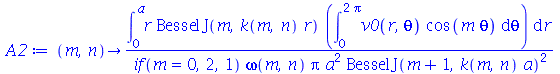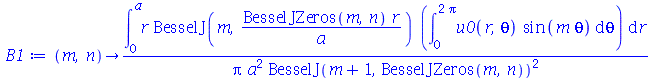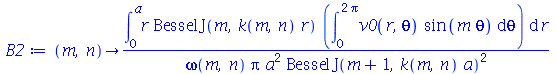Exemplo 1 - Transmissão de calor
Ref. 1: Wikipedia - Equação de calor
Ref. 2: A. O. de Morais, Transferência de calor no escoamento laminar não Newtoniano com difusividade térmica efetiva em tubos. Monografia, Universidade de São Paulo, 2012.
A equação geral da transmissão de calor é
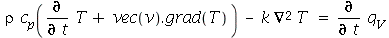
onde
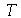 temperatura do fluido
temperatura do fluido
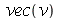 vetor velocidade do fluido
vetor velocidade do fluido
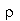 densidade do fluido
densidade do fluido
![c[p]](images/curso8_106.gif) calor específico do fluido
calor específico do fluido
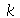 condutividade térmica do fluido
condutividade térmica do fluido
![diff(q[V], t)](images/curso8_108.gif) geração volumétrica de calor
geração volumétrica de calor
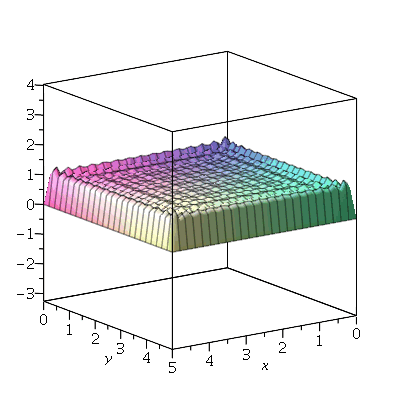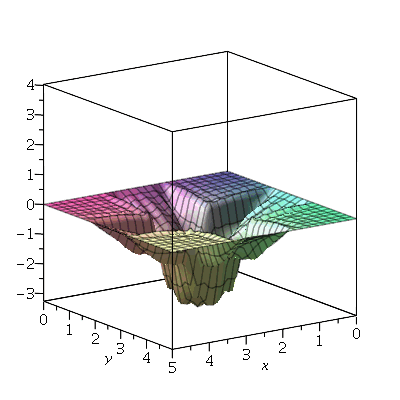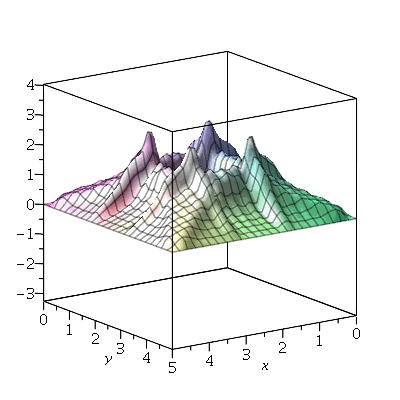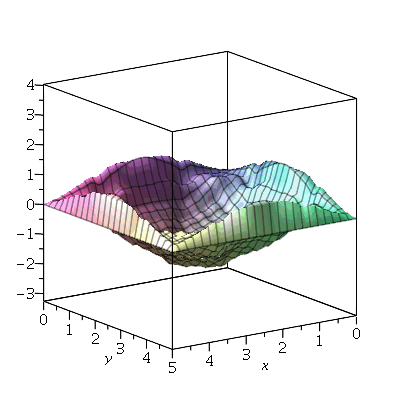
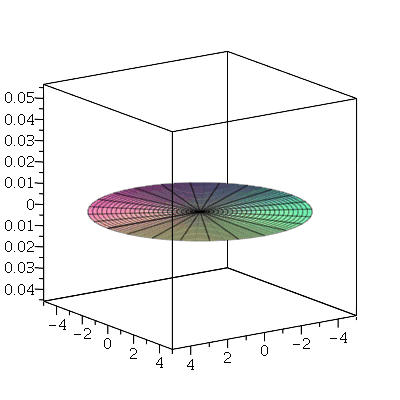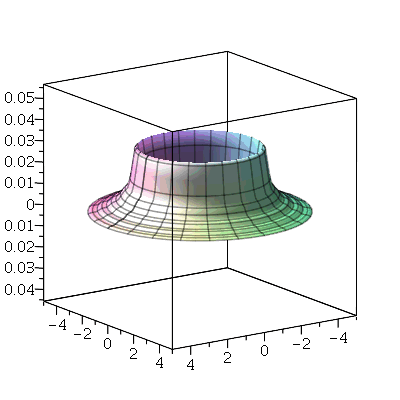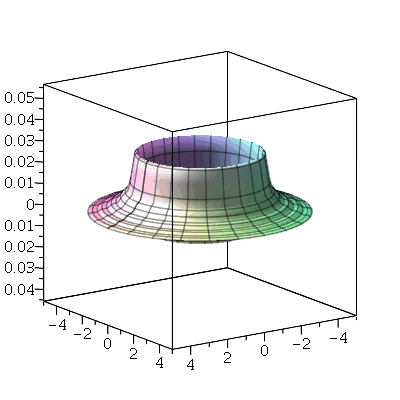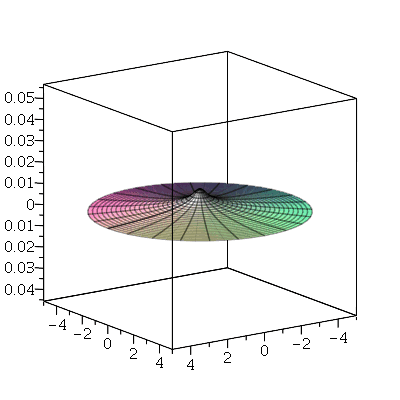
Problema Considere uma barra de comprimento 85 cm e largura 15 cm inicialmente a 37 graus centígrados isolada do meio ambiente exceto pelas suas extremidades, que são mantidas a 0 graus centígrados. Suponha que ![`*`(rho, `*`(c[p])) = 1](images/curso8_109.gif) e
e 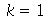 para esta barra. Encontre a temperatura da barra.
para esta barra. Encontre a temperatura da barra.
Solução: A equação que rege a evolução da temperatura em função da variável expacial 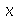 e do tempo
e do tempo 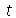 é
é
![`+`(`*`(rho, `*`(c[p], `*`(diff(T, t)))), `-`(`*`(k, `*`(diff(T, x, x))))) = 0](images/curso8_113.gif)
pois 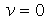 e
e ![diff(q[V], t) = 0](images/curso8_115.gif) . Vamos supor que a barra vai de
. Vamos supor que a barra vai de 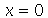 até
até 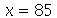 .
.
| > |
 |
| > |
 |
| > |
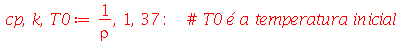 |
| > |
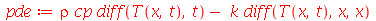 |
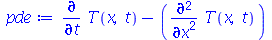 |
(1.5.1) |
As condições de contorno e as condições iniciais são
| > |
 |
| > |
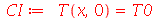 |
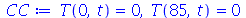 |
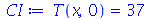 |
(1.5.2) |
A solução fornecida pelo
pdsolve
é
| > |
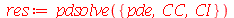 |
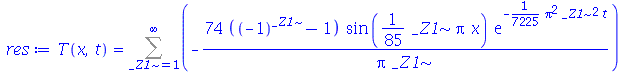 |
(1.5.3) |
Note que a solução é uma série de Fourier. Vamos fazer a seguinte aproximação. Vamos tomar um número finito (truncamento) de termos e substituir o índice mudo do somatório para a variável 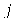 (por uma questão de elegância):
(por uma questão de elegância):
| > |
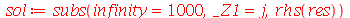 |
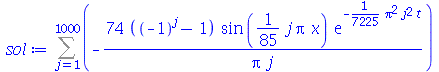 |
(1.5.4) |
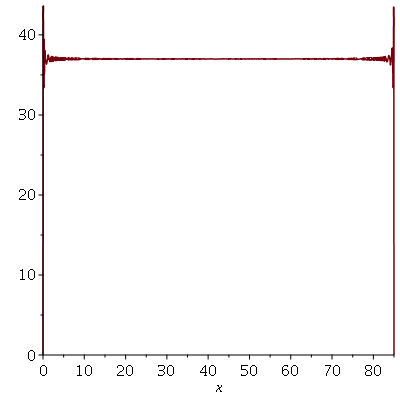
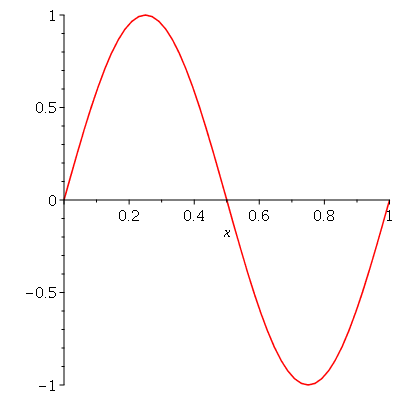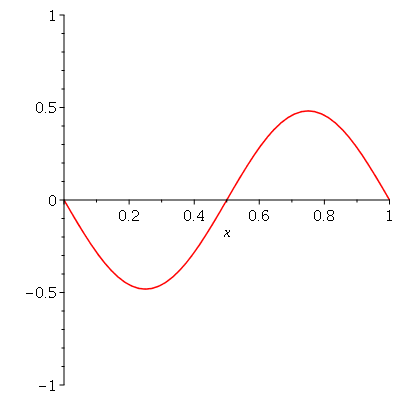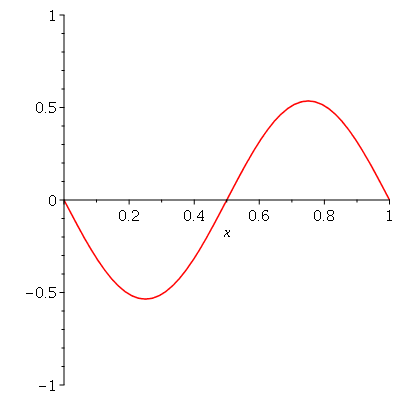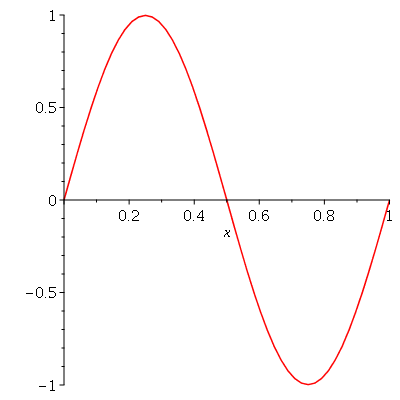
Podemos ver que para 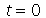 , teremos uma aproximação da condição inicial:
, teremos uma aproximação da condição inicial:
| > |
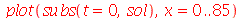 |
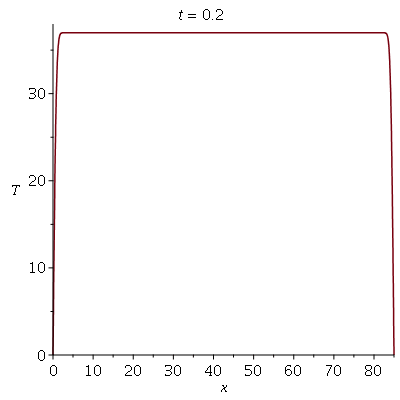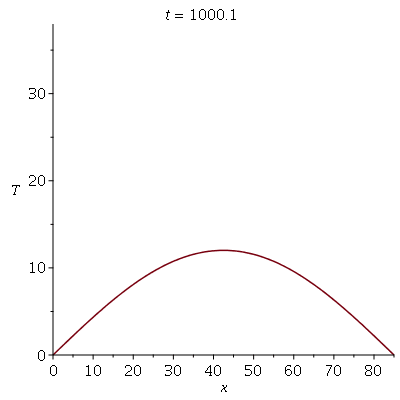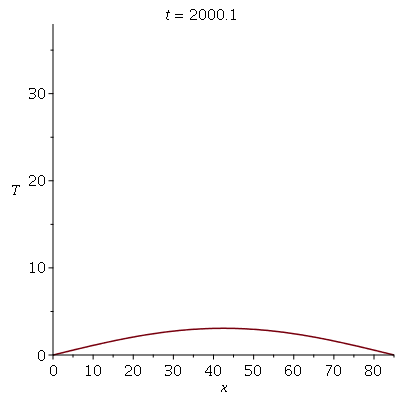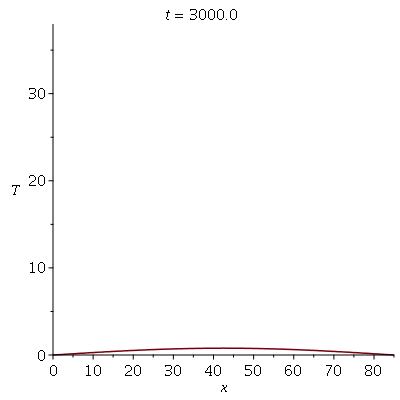
Se aumentarmos o truncamento da série de Fourier, obteremos um aproximação melhor. As oscilações da função representando a condição inicial nas extremidades da barra são chamadas de fenômeno de Gibbs e refletem a dificuldade de aproximar funções discontínuas por séries de Fourier, que são somas de funções oscilatórias contínuas.
Podemos agora animar a solução
| > |
![plots:-animate(plot, [sol, x = 0 .. 85, T = 0 .. `+`(T0, 1)], t = .2 .. 3000)](images/curso8_135.gif) |
O gráfico de densidade é bem mais elegante (Temperatura 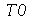 é vermelha e temperatura 0 graus centígrados é preta):
é vermelha e temperatura 0 graus centígrados é preta):
| > |

 |
Para fazer a animação usando o gráfico de densidade, é importante usar a opção
scaletorange
:
| > |

 |
 |
|
| > |
|
Exemplo 2 - Propagação de ondas em cordas
Ref.: Wikipedia - Equação da onda
Vamos considerar uma corda horizontal infinita uniformemente distentida por uma tração T. Vamos supor que as oscilações da corda são sempre na direção vertical. Sob certas restrições, como por exemplo pequenas amplitudes, a equação de onda que descreve o deslocamento vertical 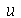 (dependente das variável espacial
(dependente das variável espacial 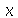 e do tempo
e do tempo 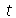 ) na ausência de forças externas é dada por:
) na ausência de forças externas é dada por:
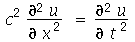
onde 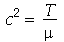 e
e 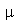 é a densidade de massa.
é a densidade de massa.
Resolução da equação de onda
Vamos atribuir a equação diferencial deste problema à variável eq_de_onda:
| > |
 |
| > |
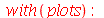 |
| > |
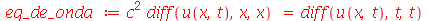 |
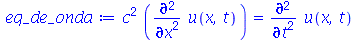 |
(1.6.1.1) |
A solução geral pode ser encontrada pelo comando
pdsolve
:
| > |
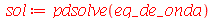 |
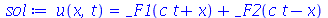 |
(1.6.1.2) |
onde 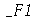 e
e 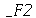 são funções genéricas. Um pulso senoidal se movendo para a direita e gerado da seguinte maneira:
são funções genéricas. Um pulso senoidal se movendo para a direita e gerado da seguinte maneira:
| > |
 |
 |
(1.6.1.3) |
| > |
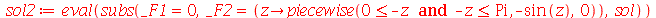 |
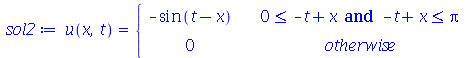 |
(1.6.1.4) |
| > |
 |
Note que a animação dura 10 unidades de tempo (por exemplo: segundos) e o pulso foi do ponto 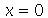 até
até 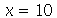 em unidades de distância (por exemplo: centímetros). Portanto, a velocidade de onda é 1 m/s. Como exercício, mude o valor de
em unidades de distância (por exemplo: centímetros). Portanto, a velocidade de onda é 1 m/s. Como exercício, mude o valor de 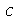 e verifique que a velocidade do pulso muda (o intervalo para
e verifique que a velocidade do pulso muda (o intervalo para 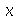 também deve ser mudado).
também deve ser mudado).
A superposição de dois pulsos senoidais se movendo em direção oposta e gerado da seguinte maneira:
| > |

 |
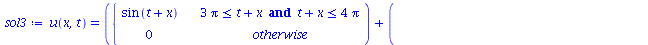
 |
(1.6.1.5) |
| > |
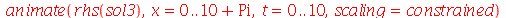 |
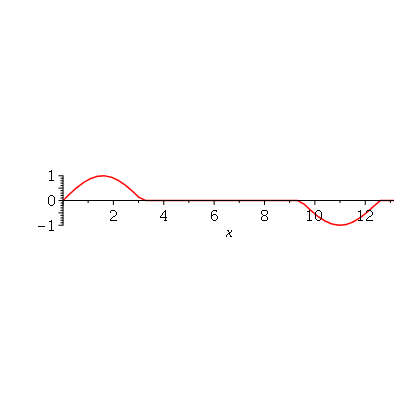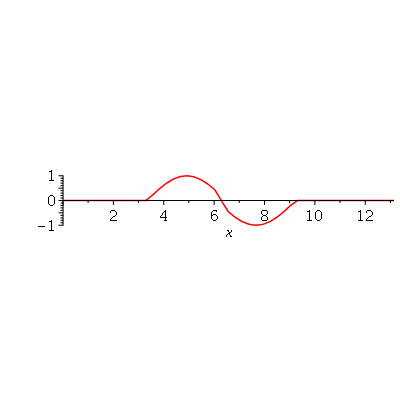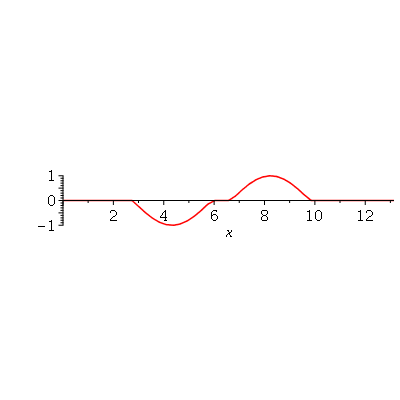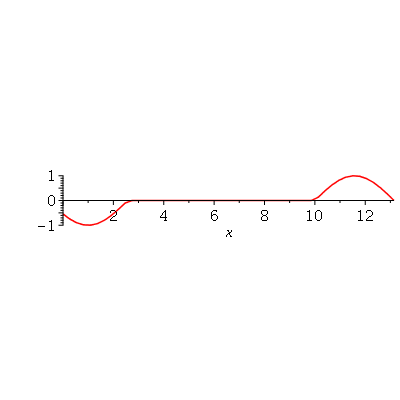 |
|
| > |
|
Se a corda estiver presa nas extremidades (em 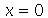 e
e 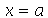 ), a equação diferencial parcial pode ser resolvida pelo método de separação de variáveis e a solução geral pode ser expressa por uma série de Fourier. A corda de comprimento a presa nas extremidades é caracterizada pelas seguintes condições de contorno:
), a equação diferencial parcial pode ser resolvida pelo método de separação de variáveis e a solução geral pode ser expressa por uma série de Fourier. A corda de comprimento a presa nas extremidades é caracterizada pelas seguintes condições de contorno:  e
e 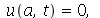 para
para 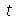 gerérico.Vamos resolver a equação de onda usando o método de separação de variáveis. Vamos supor que
gerérico.Vamos resolver a equação de onda usando o método de separação de variáveis. Vamos supor que 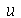 é uma função separável nas variáveis
é uma função separável nas variáveis 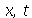 , isto é,
, isto é, 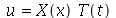 :
:
| > |
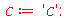 |
| > |
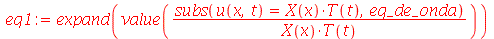 |
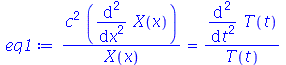 |
(1.6.1.6) |
Cada termo da expressão acima deve ser constante, pois cada um é função de uma variável independente. Vamos selecionar o termo dependente de 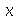 , e igualar a uma constante :
, e igualar a uma constante :
| > |
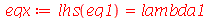 |
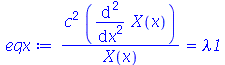 |
(1.6.1.7) |
A equação diferencial acima pode ter soluções oscilatórias, lineares ou exponenciais dependendo se a constante for negativa, zero ou positiva, respectivamente (exercício: resolva a EDO acima para 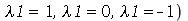 . Para que as condições de contorno sejam satisfeitas, isto é,
. Para que as condições de contorno sejam satisfeitas, isto é, 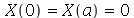 , temos que impor que a constante
, temos que impor que a constante 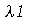 seja negativa:
seja negativa:
| > |
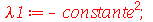 |
 |
(1.6.1.8) |
| > |
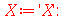 |
| > |
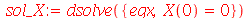 |
 |
(1.6.1.9) |
Para a condição de contorno 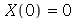 ser satisfeita, vamos impor a condição de contorno
ser satisfeita, vamos impor a condição de contorno 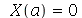 .
.
| > |
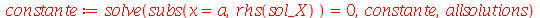 |
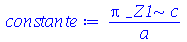 |
(1.6.1.10) |
| > |
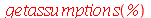 |
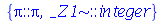 |
(1.6.1.11) |
Note que 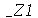 tem que ser um número inteiro.
tem que ser um número inteiro.
| > |
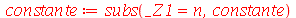 |
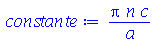 |
(1.6.1.12) |
onde n é um inteiro positivo (no lugar de 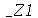 ).
).
Vamos eliminar a constante arbitrária por enquanto:
| > |
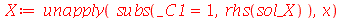 |
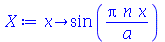 |
(1.6.1.13) |
A equação diferencial para a função dependente da variável t é obtida da seguinte forma:
| > |
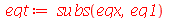 |
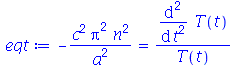 |
(1.6.1.14) |
cuja solução geral é:
| > |
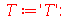 |
| > |
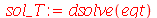 |
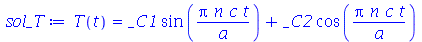 |
(1.6.1.15) |
Vamos colocar esta solução numa forma mais conveniente:
| > |
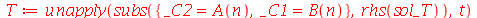 |
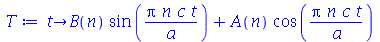 |
(1.6.1.16) |
onde A e B são constantes que podem depender dos autovalores m e n. Vamos definir a frequência do modo normal <n>:
| > |
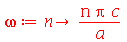 |
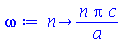 |
(1.6.1.17) |
e definir os modos normais como uma função de m e n. Existem duas possibilidades que são:
| > |
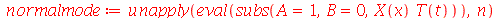 |
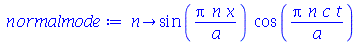 |
(1.6.1.18) |
| > |
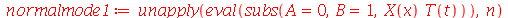 |
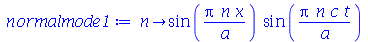 |
(1.6.1.19) |
Uma vez que a equação diferencial do movimento da corda é linear e homogênea, a solução geral é uma superposição de todas as soluções linearmente independentes possíveis. Assim, tomaremos o somatório sobre todos os valores de m e n:
| > |
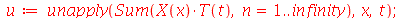 |
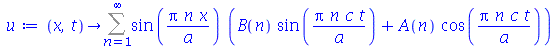 |
(1.6.1.20) |
As constantes arbitrárias 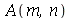 e
e 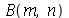 são determinadas a partir das condições iniciais. Geralmente são elas a posição inicial
são determinadas a partir das condições iniciais. Geralmente são elas a posição inicial 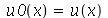 e a velocidade inicial
e a velocidade inicial )(x, 0)](images/curso8_226.gif) .
.
Animação dos Modos Normais
Os modos normais podem ser animados como a função animate. Vamos construir a função animate_mode, que anima o modo especificado pelos seus argumentos. Por exemplo, animate_mode(2) faz a animação do modo n=2.
| > |
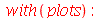 |
| > |
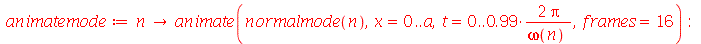 |
Para fazer a animação de um determinado modo, temos que dar valores numéricos para os parâmetros a, b e c. Vamos supor que o comprimento é a=1, a largura é b=1 e a constante c=1 em um certo sistema de unidades:
| > |
 |
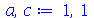 |
(1.6.2.1) |
Vamos fazer a animação do modo 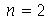 :
:
| > |
 |
Vejamos a animação do modo 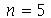 :
:
| > |
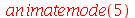 |
Os pontos que ficam imóveis são chamados pontos nodais.
Animação com Condições Iniciais
Encontramos anteriormente a função 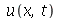 que descreve o movimento vertical da corda de comprimento
que descreve o movimento vertical da corda de comprimento 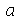 presa nas extremidades. Esta solução é uma série de Fourier. Uma vez que os modos normais com pequenos valores de
presa nas extremidades. Esta solução é uma série de Fourier. Uma vez que os modos normais com pequenos valores de 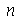 dominam sobre os que tem grandes valores, podemos truncar o somatório. O ponto de truncagem satisfatório depende das condições iniciais do problema. Vamos converter o somatório infinito num somatório finito com
dominam sobre os que tem grandes valores, podemos truncar o somatório. O ponto de truncagem satisfatório depende das condições iniciais do problema. Vamos converter o somatório infinito num somatório finito com 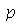 termos e definir a função
termos e definir a função 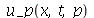 da seguinte forma:
da seguinte forma:
| > |
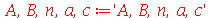 |
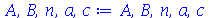 |
(1.6.3.1) |
| > |
 |
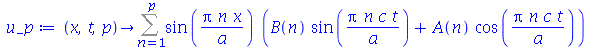 |
(1.6.3.2) |
As constantes 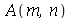 e
e 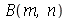 , que aparecem na função
, que aparecem na função 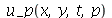 , podem ser obtidas a partir das condições iniciais posição inicial
, podem ser obtidas a partir das condições iniciais posição inicial 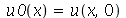 e velocidade inicial
e velocidade inicial )(x, 0)](images/curso8_250.gif) usando as seguintes fórmulas:
usando as seguintes fórmulas: 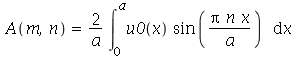 e
e 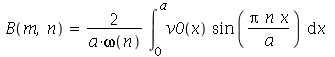 (veja referências sobre inversão de séries de Fourier, por exemplo, E. Butkov, Física Matemática, cap. 4).
(veja referências sobre inversão de séries de Fourier, por exemplo, E. Butkov, Física Matemática, cap. 4).
| > |
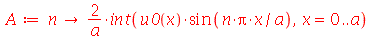 |
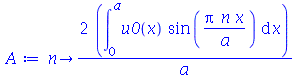 |
(1.6.3.3) |
| > |
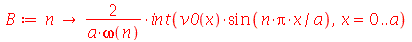 |
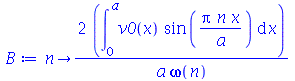 |
(1.6.3.4) |
Antes de fazer a animação com condições iniciais, vamos calcular as contantes 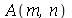 e
e 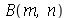 para
para 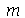 e
e 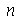 inteiros positivos genéricos. É mais eficiente calcular estas constantes para
inteiros positivos genéricos. É mais eficiente calcular estas constantes para 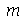 e
e 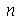 genéricos e depois substituir valores numéricos, do que calcular diretamente para diversos valores numéricos de
genéricos e depois substituir valores numéricos, do que calcular diretamente para diversos valores numéricos de 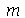 e
e 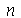 . Vamos usar as seguintes condições iniciais:
. Vamos usar as seguintes condições iniciais:
| > |
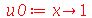 |
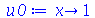 |
(1.6.3.5) |
| > |
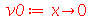 |
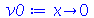 |
(1.6.3.6) |
| > |
 |
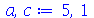 |
(1.6.3.7) |
Para calcular 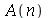 e
e 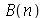 para
para 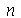 inteiro positivo genérico, vamos usar a função assume. Desta forma, o comando simplify das funções
inteiro positivo genérico, vamos usar a função assume. Desta forma, o comando simplify das funções 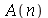 e
e 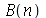 poderá fazer as simplificações pertinentes:
poderá fazer as simplificações pertinentes:
| > |
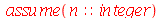 |
| > |
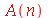 |
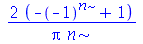 |
(1.6.3.8) |
| > |
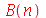 |
 |
(1.6.3.9) |
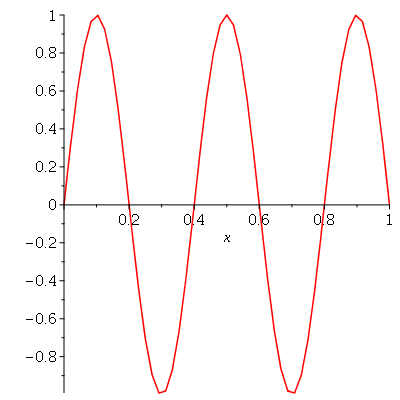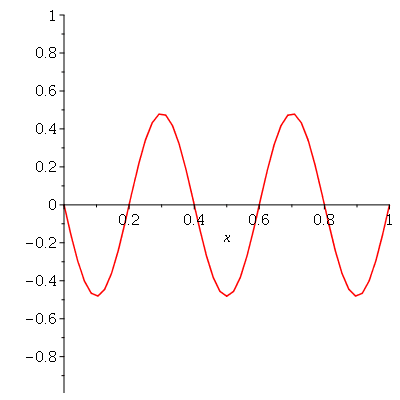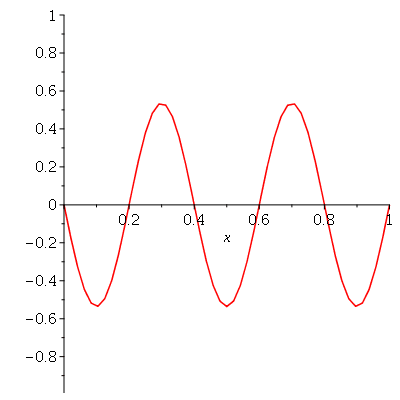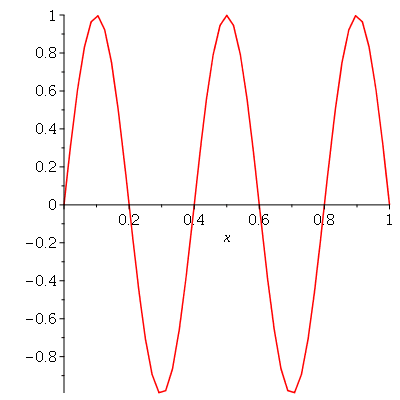
Vamos fazer o gráfico da posição inicial da corda desta vez descrita pela função 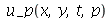 , pois a partir dela podemos achar um bom valor para a constante
, pois a partir dela podemos achar um bom valor para a constante 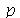 , por comparação com o gráfico obtido diretamente de
, por comparação com o gráfico obtido diretamente de 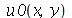 . Observe que para
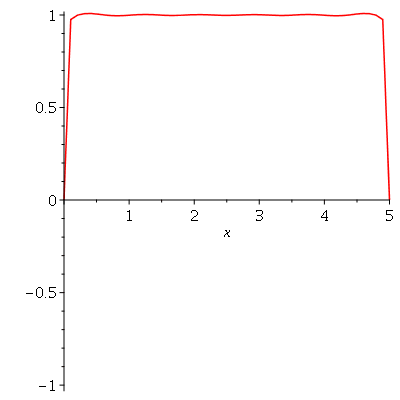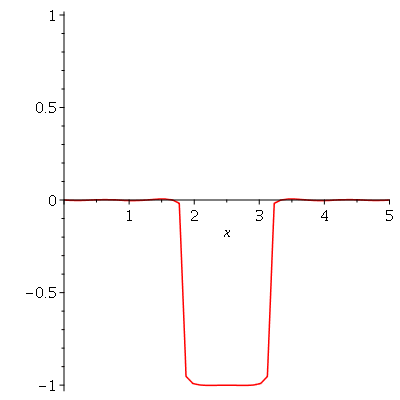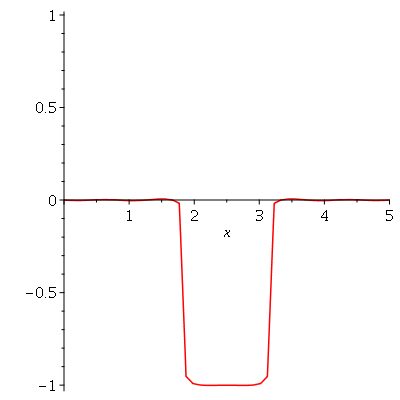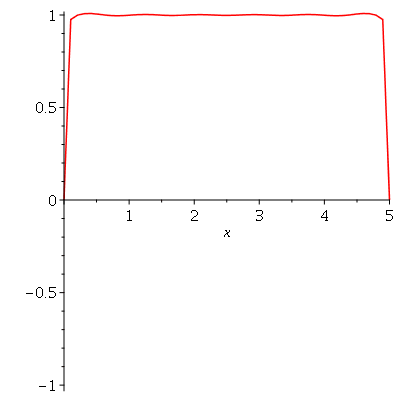
. Observe que para 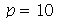 a série de Fourier truncada aproxima razoavelmente bem a posição inicial da corda:
a série de Fourier truncada aproxima razoavelmente bem a posição inicial da corda:
| > |
 |
Assim, o valor 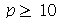 é satisfatório para esse tipo de condições iniciais. Note exite uma ondulação na parte superior do gráfico. Isto é consquência do truncamento da série de Fourier dupla. Esta ondulação só desparece a rigor, no limite quando
é satisfatório para esse tipo de condições iniciais. Note exite uma ondulação na parte superior do gráfico. Isto é consquência do truncamento da série de Fourier dupla. Esta ondulação só desparece a rigor, no limite quando 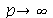 . Outro detalhe que podemos observar, é que a série truncada obedece às condicões de contorno, enquanto que a condição inicial não obedece (veja a expressão de
. Outro detalhe que podemos observar, é que a série truncada obedece às condicões de contorno, enquanto que a condição inicial não obedece (veja a expressão de 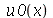 ). Esta discrepância também só desaparece quando
). Esta discrepância também só desaparece quando 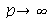 . As oscilações da função representando a condição inicial nas extremidades da barra são chamadas de fenômeno de Gibbs e refletem a dificuldade de aproximar funções discontínuas por séries de Fourier, que são somas de funções oscilatórias contínuas.
. As oscilações da função representando a condição inicial nas extremidades da barra são chamadas de fenômeno de Gibbs e refletem a dificuldade de aproximar funções discontínuas por séries de Fourier, que são somas de funções oscilatórias contínuas.
A função a seguir faz a animação do movimento da corda descrita pela função 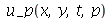 . O primeiro argumento é o tempo de animação e o segundo é o número
. O primeiro argumento é o tempo de animação e o segundo é o número 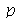 que representa a truncagem do somatório duplo:
que representa a truncagem do somatório duplo:
| > |
 |
| > |

 |
Para as condições iniciais descritas acima, a animação do movimento da corda com duas oscilações dominantes e 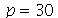 é:
é:
| > |

 |
Vamos fazer a animação no caso em que a corda está parada na posição horizontal, e sofre um impulso de cima para baixo em seu centro:
| > |
 |
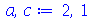 |
(1.6.3.10) |
| > |
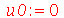 |
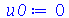 |
(1.6.3.11) |
| > |
 |
 |
(1.6.3.12) |
Como antes, vamos calcular 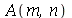 e
e 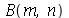 com
com 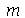 e
e 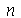 inteiros positivos genéricos:
inteiros positivos genéricos:
| > |
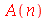 |
 |
(1.6.3.13) |
| > |
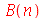 |
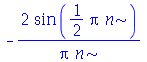 |
(1.6.3.14) |
Vamos fazer a animação durante um tempo 5 e truncar o somatório em 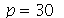 com 40 frames:
com 40 frames:
| > |
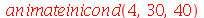 |
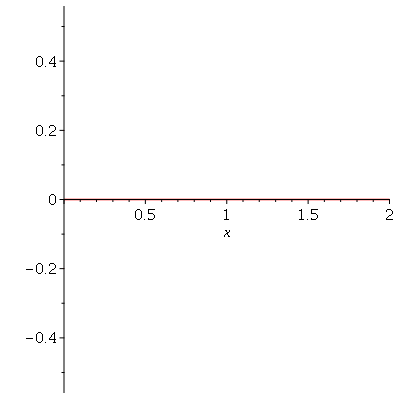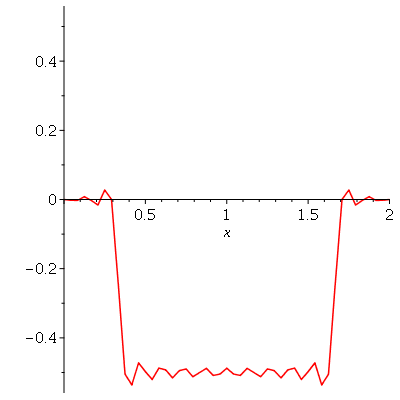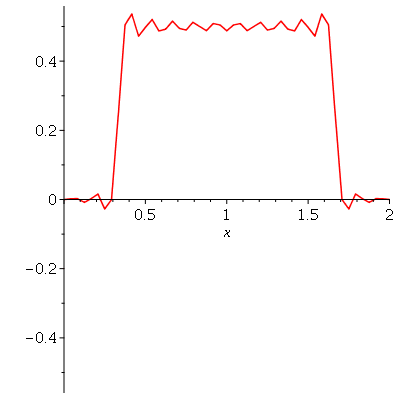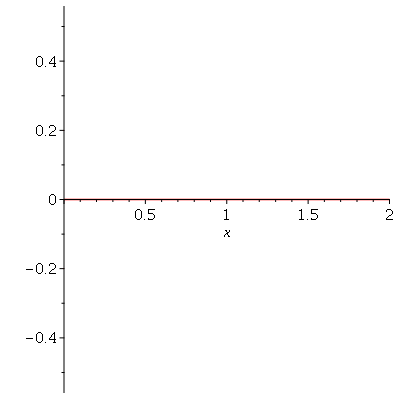 |
|
| > |
|
Exercícios
1) Verifique que normalmode, normalmode1 e 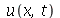 satisfazem a equação de onda.
satisfazem a equação de onda.
2) a) Resolva a equação de onda para uma corda obedecendo às seguintes condições de contorno: Uma extremidade da corda está presa e a outra está livre. [Sug.: Quando a extremidade está livre, a derivada de 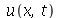 deve se anular.]
deve se anular.]
b) Obtenha os modos normais e a solução geral obedecendo às condições iniciais genéricas.
c) Faça a animação dos modos normais.
d) Faça a animação com diversas condições iniciais.
Exemplo 3 - Oscilação de membranas usando séries de Fourier
Ref.: R. Portugal, L. Golebiowski, D. Frenkel. Oscillation of membranes using computer algebra. American Journal of Physics 67 (6), 534-537, 1999.
Vamos considerar uma membrana horizontal uniformemente distentida em todas as direções por uma tração T. A forma da membrana será especificada pelas condições de contorno. Qualquer que seja a forma, vamos analisar o caso em que toda a borda da membrana está fixa. As oscilações são sempre na direção vertical. Sob certas restrições, como por exemplo pequenas oscilações, a equação de onda que descreve o deslocamento vertical 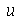 (dependente das variáveis espaciais e do tempo) na ausência de forças externas é dada por:
(dependente das variáveis espaciais e do tempo) na ausência de forças externas é dada por:
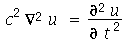
onde 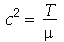 e
e 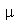 é a densidade de massa. Esta equação diferencial parcial pode ser resolvida pelo método de separação de variáveis e a solução geral pode ser expressa por uma série de Fourier generalizada. No caso da membrana retangular, a solução é uma série de Fourier tripla usual e no caso da membrana circular axialmente simétrica, a solução é uma série de Fourier-Bessel na parte espacial e Fourier usual na parte temporal. Vamos analisar o movimento oscilatório destes destes dois tipos de membranas.
é a densidade de massa. Esta equação diferencial parcial pode ser resolvida pelo método de separação de variáveis e a solução geral pode ser expressa por uma série de Fourier generalizada. No caso da membrana retangular, a solução é uma série de Fourier tripla usual e no caso da membrana circular axialmente simétrica, a solução é uma série de Fourier-Bessel na parte espacial e Fourier usual na parte temporal. Vamos analisar o movimento oscilatório destes destes dois tipos de membranas.
Membrana Retangular
Resolução da equação de onda
A membrana retangular de comprimento a e largura b presa nas bordas é caracterizada pelas seguintes condições de contorno: 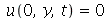 e
e 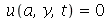 para
para 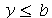 e
e 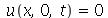 e
e 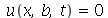 para
para 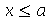 . Vamos atribuir a equação diferencial deste problema à variável eq_de_onda:
. Vamos atribuir a equação diferencial deste problema à variável eq_de_onda:
| > |
 |
| > |
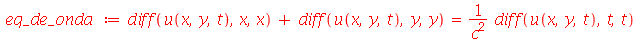 |
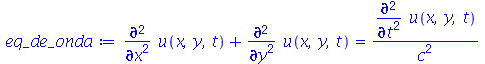 |
(1.7.1.1.1) |
| > |
 |
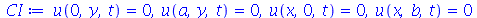 |
(1.7.1.1.2) |
Vamos resolver essa equação usando o método de separação de variáveis. Vamos supor que 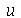 é uma função separável nas variáveis
é uma função separável nas variáveis 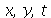 , isto é,
, isto é, 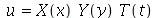 :
:
| > |
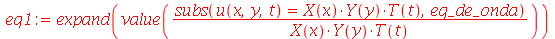 |
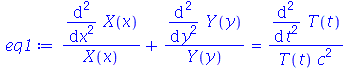 |
(1.7.1.1.3) |
Cada termo da expressão acima deve ser constante, pois cada um é função de uma variável independente. Vamos selecionar o termo dependente de 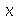 , e igualar a uma constante :
, e igualar a uma constante :
| > |
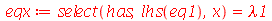 |
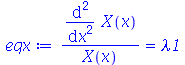 |
(1.7.1.1.4) |
A equação diferencial acima pode ter soluções oscilatórias, lineares ou exponenciais dependendo se a constante for negativa, zero ou positiva, respectivamente. Para que as condições de contorno sejam satisfeitas, isto é, 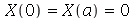 , temos que impor que a constante
, temos que impor que a constante 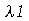 seja negativa e que ela assuma valores discretos dados por:
seja negativa e que ela assuma valores discretos dados por:
| > |
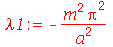 |
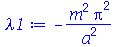 |
(1.7.1.1.5) |
onde m é um inteiro positivo. A solução geral da equação da parte é:
| > |
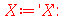 |
| > |
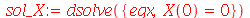 |
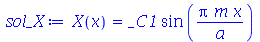 |
(1.7.1.1.6) |
Vamos eliminar a constante arbitrária por enquanto:
| > |
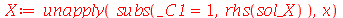 |
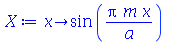 |
(1.7.1.1.7) |
Vamos repetir o mesmo procedimento para o termo dependente de y:
| > |
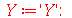 |
| > |
 |
| > |
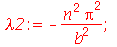 |
| > |
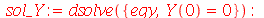 |
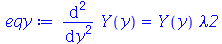 |
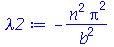 |
(1.7.1.1.8) |
| > |
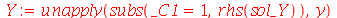 |
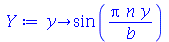 |
(1.7.1.1.9) |
A equação diferencial para a função dependente da variável t é obtida da seguinte forma:
| > |
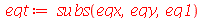 |
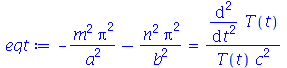 |
(1.7.1.1.10) |
cuja solução geral é:
| > |
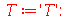 |
| > |
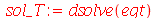 |
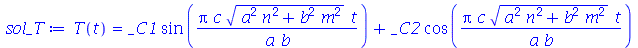 |
(1.7.1.1.11) |
Vamos colocar esta solução numa forma mais conveniente:
| > |
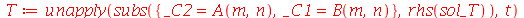 |
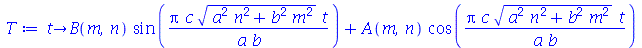 |
(1.7.1.1.12) |
onde A e B são constantes que podem depender dos autovalores m e n. Vamos definir a frequência do modo normal <>:
| > |
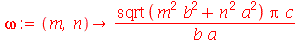 |
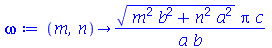 |
(1.7.1.1.13) |
e definir os modos normais como uma função de m e n. Existem duas possibilidades que são:
| > |
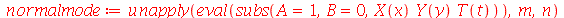 |
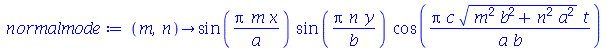 |
(1.7.1.1.14) |
| > |
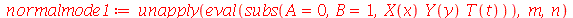 |
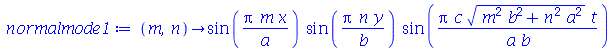 |
(1.7.1.1.15) |
Uma vez que a equação diferencial do movimento da membrana é linear e homogênea, a solução geral é uma superposição de todas as soluções linearmente independentes possíveis. Assim, tomaremos o somatório sobre todos os valores de m e n:
| > |
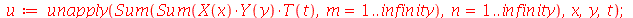 |
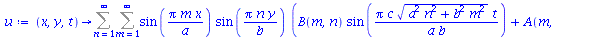
 |
(1.7.1.1.16) |
As constantes arbitrárias 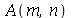 e
e 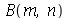 são determinadas a partir das condições iniciais. Geralmente são elas a posição inicial
são determinadas a partir das condições iniciais. Geralmente são elas a posição inicial 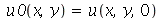 e a velocidade inicial
e a velocidade inicial )(x, y, 0)](images/curso8_378.gif) .
.
Animação dos Modos Normais
Os modos normais podem ser animados como a função animate3d. Vamos construir a função animate_mode, que anima o modo especificado pelos seus argumentos. Por exemplo, animate_mode(1,2) faz a animação do modo m=1 e n=2.
| > |
 |
| > |
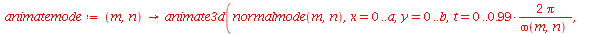
 |
Para fazer a animação de um determinado modo, temos que dar valores numéricos para os parâmetros a, b e c. Vamos supor que o comprimento é a=1, a largura é b=1 e a constante c=1 em um certo sistema de unidades:
| > |
  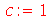 |
Vamos fazer a animação do modo <1,2>
| > |
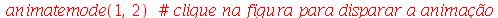 |
As linhas nodais são curvas cujos pontos se mantêm em repouso durante todo instante. Por exemplo, vejamos a animação do modo <2,5>:
| > |
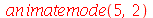 |
Podemos ver que há 4 retas nodais paralelas ao eixo y e 1 reta nodal paralela ao eixo x. Esta característica pode ser generalizada para qualquer modo de vibração. O modo <m,n> tem m-1 retas nodais paralelas ao eixo y e n-1 retas nodais paralelas ao eixo x. Em geral, as linhas nodais nem sempre são retas. Abaixo, mostraremos um exemplo de uma linha nodal fechada aproximadamente circular em uma membrana quadrada. Isso ocorre quando existe degenerescência.
Análise da Degenerescência
Num modo normal de vibração, todos os pontos da membrana vibram com a mesma frequência; cada modo normal tem um frequência característica 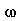
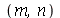 . Se a membrana for quadrada, dois modos normais diferentes podem oscilar com a mesma frequência. Por exemplo, para a membrana quadrada de largura de uma unidade, os modos <1,2> e <2,1> têm a mesma frequência:
. Se a membrana for quadrada, dois modos normais diferentes podem oscilar com a mesma frequência. Por exemplo, para a membrana quadrada de largura de uma unidade, os modos <1,2> e <2,1> têm a mesma frequência:
| > |
 |
| > |
 |
| > |
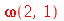 |
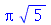 |
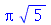 |
(1.7.1.3.1) |
Neste caso, qualquer combinação linear destes modos de vibração também vai oscilar na mesma frequência. Este fenômeno é chamado de degenerescência. Isto ocorre sempre que um autovalor (a frequência) é degenerado, possuindo mais de um autovetor associado (o modo normal). A função a seguir faz a animação da combinação linear 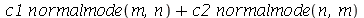 .
.
| > |

 |
Vamos considerar uma membrana quadrada:
| > |
 |
 |
(1.7.1.3.2) |
Vamos fazer a animação da combinação linear 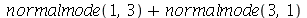 , onde podemos verificar que a linha nodal é uma curva fechada:
, onde podemos verificar que a linha nodal é uma curva fechada:
| > |
 |
A combinação linear 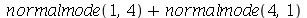 tem como linha nodal uma curva fechada e uma reta (uma das diagonais da membrana):
tem como linha nodal uma curva fechada e uma reta (uma das diagonais da membrana):
| > |
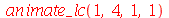 |
A linha nodal é descrita pela equação 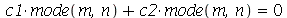 . Esta equação depende das variáveis x e y. O fator temporal é comum aos dois termos e portanto é cancelado. Através do comando implicitplot, podemos fazer o gráfico da curva y contra x mesmo sem resolver explicitamente a equação. A função nodal_line a seguir faz o desenho da linha nodal. Os argumentos desta função são iguais ao do função
. Esta equação depende das variáveis x e y. O fator temporal é comum aos dois termos e portanto é cancelado. Através do comando implicitplot, podemos fazer o gráfico da curva y contra x mesmo sem resolver explicitamente a equação. A função nodal_line a seguir faz o desenho da linha nodal. Os argumentos desta função são iguais ao do função  .
.
| > |

 |
A linha nodal dos dois últimos exemplos que vimos acima são:
| > |
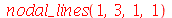 |
e
| > |
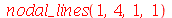 |
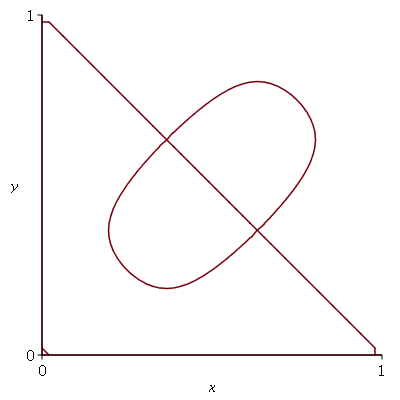 |
|
Animação com Condições Iniciais
Encontramos anteriormente a função 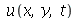 que descreve o movimento vertical da membrana retangular de largura
que descreve o movimento vertical da membrana retangular de largura 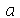 e comprimento
e comprimento 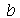 presa nas bordas. Esta solução é uma série de Fourier dupla. Uma vez que os modos normais com pequenos valores de
presa nas bordas. Esta solução é uma série de Fourier dupla. Uma vez que os modos normais com pequenos valores de 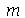 e
e 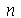 dominam sobre os que tem grandes valores, podemos truncar o somatório duplo. O ponto de truncagem satisfatório depende das condições iniciais do problema. Vamos converter o somatório infinito num somatório finito com
dominam sobre os que tem grandes valores, podemos truncar o somatório duplo. O ponto de truncagem satisfatório depende das condições iniciais do problema. Vamos converter o somatório infinito num somatório finito com 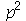 termos e definir a função
termos e definir a função 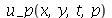 da seguinte forma:
da seguinte forma:
| > |
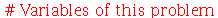 |
| > |
 |
| > |
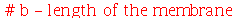 |
| > |
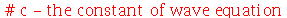 |
| > |
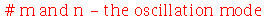 |
| > |
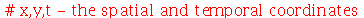 |
| > |
 |
| > |
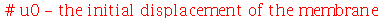 |
| > |
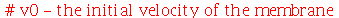 |
| > |
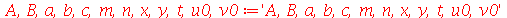 |
 |
(1.7.1.4.1) |
| > |
 |
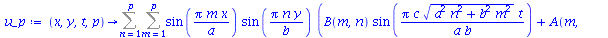
 |
(1.7.1.4.2) |
As constantes 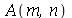 e
e 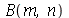 , que aparecem na função
, que aparecem na função 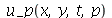 , podem ser obtidas a partir das condições iniciais posição inicial
, podem ser obtidas a partir das condições iniciais posição inicial 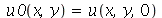 e velocidade inicial
e velocidade inicial )(x, y, 0)](images/curso8_443.gif) usando as seguintes fórmulas:
usando as seguintes fórmulas: ![A(m, n) = `+`(`/`(`*`(4, `*`(int(`*`(u0(x, y), `*`(sin(`/`(`*`(Pi, `*`(m, `*`(x))), `*`(a))), `*`(sin(`/`(`*`(Pi, `*`(n, `*`(y))), `*`(b)))))), [x = 0 .. a, y = 0 .. b]))), `*`(a, `*`(b))))](images/curso8_444.gif) e
e ![B(m, n) = `+`(`/`(`*`(4, `*`(int(`*`(v0(x, y), `*`(sin(`/`(`*`(Pi, `*`(m, `*`(x))), `*`(a))), `*`(sin(`/`(`*`(Pi, `*`(n, `*`(y))), `*`(b)))))), [x = 0 .. a, y = 0 .. b]))), `*`(a, `*`(b, `*`(omega(m, ...](images/curso8_445.gif) (veja referências sobre inversão de séries de Fourier).
(veja referências sobre inversão de séries de Fourier).
| > |
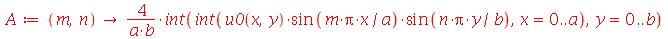 |
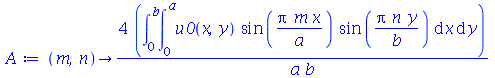 |
(1.7.1.4.3) |
| > |
 |
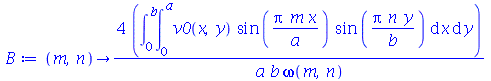 |
(1.7.1.4.4) |
Antes de fazer a animação com condições iniciais, vamos calcular as contantes 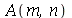 e
e 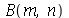 para
para 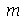 e
e 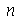 inteiros positivos genéricos. É mais eficiente calcular estas constantes para
inteiros positivos genéricos. É mais eficiente calcular estas constantes para 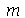 e
e 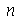 genéricos e depois substituir valores numéricos, do que calcular diretamente para diversos valores numéricos de
genéricos e depois substituir valores numéricos, do que calcular diretamente para diversos valores numéricos de 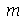 e
e 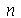 . Vamos usar as seguintes condições iniciais:
. Vamos usar as seguintes condições iniciais:
| > |
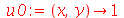 |
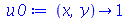 |
(1.7.1.4.5) |
| > |
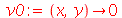 |
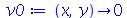 |
(1.7.1.4.6) |
| > |
 |
 |
(1.7.1.4.7) |
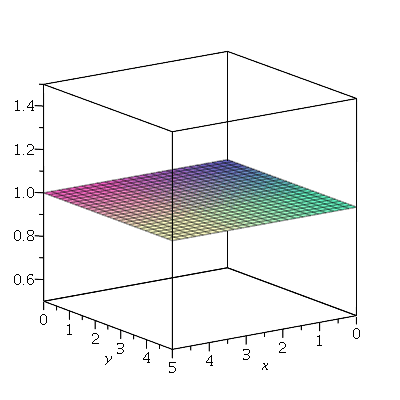
O gráfico da posição inicial é:
| > |
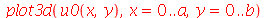 |
Para calcular 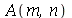 e
e 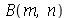 para
para 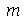 e
e 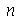 inteiros positivos genéricos, vamos usar a função assume. Desta forma, o comando simplify das funções
inteiros positivos genéricos, vamos usar a função assume. Desta forma, o comando simplify das funções 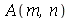 e
e 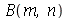 poderá fazer as simplificações pertinentes:
poderá fazer as simplificações pertinentes:
| > |
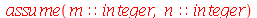 |
| > |
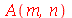 |
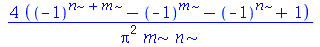 |
(1.7.1.4.8) |
| > |
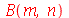 |
 |
(1.7.1.4.9) |
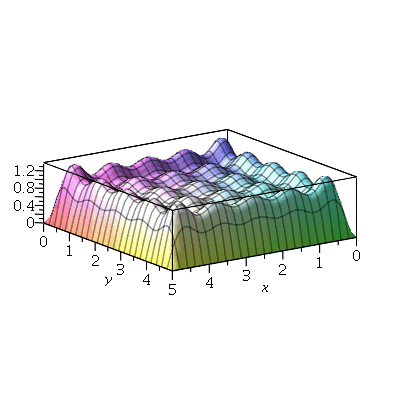
Vamos fazer o gráfico da posição inicial da membrana desta vez descrita pela função 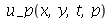 , pois a partir dela podemos achar um bom valor para a constante
, pois a partir dela podemos achar um bom valor para a constante 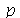 , por comparação com o gráfico obtido diretamente de
, por comparação com o gráfico obtido diretamente de 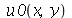 . Observe que para
. Observe que para 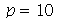 a série de Fourier truncada aproxima razoavelmente bem a posição inicial da membrana:
a série de Fourier truncada aproxima razoavelmente bem a posição inicial da membrana:
| > |
 |
Assim, o valor 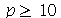 é satisfatório para esse tipo de condições iniciais. Note exite uma ondulação na parte superior do gráfico. Isto é consquência do truncamento da série de Fourier dupla. Esta ondulação só desparece a rigor, no limite quando
é satisfatório para esse tipo de condições iniciais. Note exite uma ondulação na parte superior do gráfico. Isto é consquência do truncamento da série de Fourier dupla. Esta ondulação só desparece a rigor, no limite quando 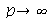 . Outro detalhe que podemos observar, é que a série truncada obedece as condicões de contorno, enquanto que a condição inicial não obedece. Esta discrepância também só desaparece quando
. Outro detalhe que podemos observar, é que a série truncada obedece as condicões de contorno, enquanto que a condição inicial não obedece. Esta discrepância também só desaparece quando 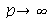 .
.
A função a seguir faz a animação do movimento da membrana descrita pela função 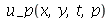 . O primeiro argumento é o tempo de animação e o segundo é o número
. O primeiro argumento é o tempo de animação e o segundo é o número 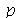 que representa a truncagem do somatório duplo:
que representa a truncagem do somatório duplo:
| > |
 |
| > |
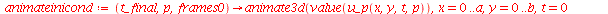
 |
Para as condições iniciais descritas acima, a animação do movimento da membrana com duas oscilações dominantes e 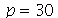 é:
é:
| > |

 |
Vamos fazer a animação no caso em que a membrana está parada na posição horizontal, e sofre um impulso de cima para baixo em seu centro:
| > |
 |
 |
(1.7.1.4.10) |
| > |
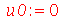 |
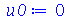 |
(1.7.1.4.11) |
| > |
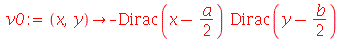 |
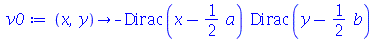 |
(1.7.1.4.12) |
Como antes, vamos calcular 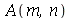 e
e 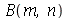 com
com 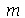 e
e 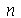 inteiros positivos genéricos:
inteiros positivos genéricos:
| > |
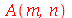 |
 |
(1.7.1.4.13) |
| > |
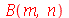 |
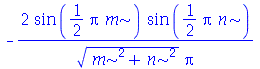 |
(1.7.1.4.14) |
Vamos fazer a animação durante um tempo 5 e truncar o somatório em 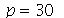 (900 termos) com 20 frames:
(900 termos) com 20 frames:
| > |
 |
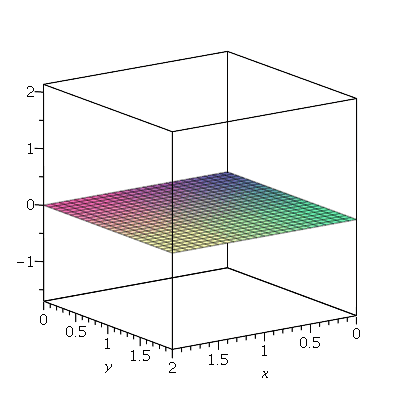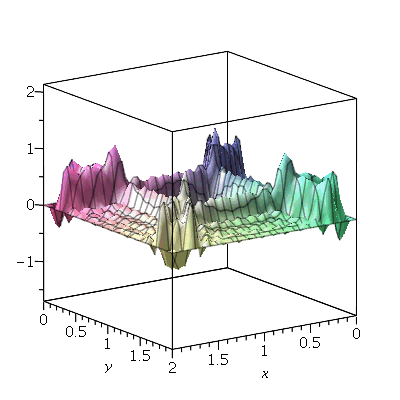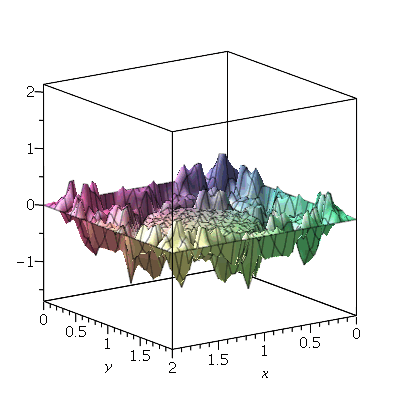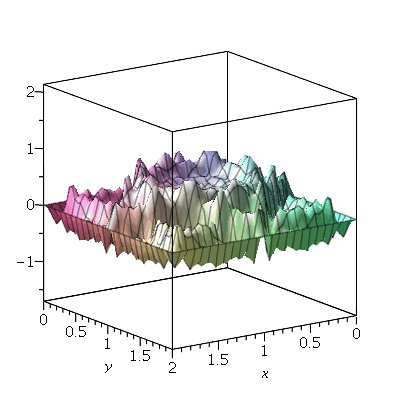 |
|
| > |
|
Exercícios
1) Verifique que normalmode, normalmode1 e 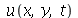 satisfazem a equação de onda.
satisfazem a equação de onda.
2) Use o comando pdsolve para encontrar a solução 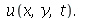 O comando dsolve não deve ser usado em nenhum momento.
O comando dsolve não deve ser usado em nenhum momento.
3) a) Resolva a equação de onda para uma membrana obedecendo às seguintes condições de contorno: Duas extremidades opostas da membrana estão presas, e as outras duas estão livres. [Sug.: Quando a extremidade está livre, a derivada de 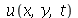 deve se anular.]
deve se anular.]
b) Obtenha os modos normais e a solução geral obedecendo às condições iniciais genéricas.
c) Faça a animação dos modos normais.
d) Faça uma análise da degenerescência.
e) Faça a animação com diversas condições iniciais.
Membrana Circular
Resolução da Equação de Onda
A membrana circular de raio a presa na borda é caracterizada pela seguinte condição de contorno em coordenadas cilíndricas: 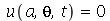 , para
, para 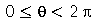 . Vamos atribuir a equação diferencial deste problema à variável wave_eq:
. Vamos atribuir a equação diferencial deste problema à variável wave_eq:
| > |
 |
| > |
, [r, theta, z], coords = cylindrical) = `/`(`*`(diff(u(r, theta, t), t, t)), `*`(`^`(c, 2)))](images/curso8_518.gif) |
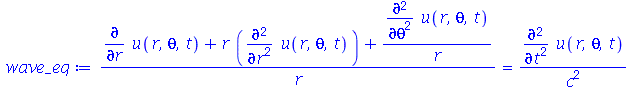 |
(1.7.2.1.1) |
Vamos resolver essa equação usando o método de separação de variáveis. Substituindo 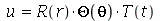 na variável
na variável 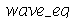 obtemos:
obtemos:
| > |
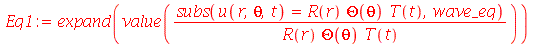 |
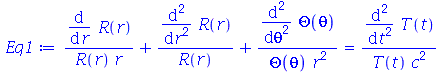 |
(1.7.2.1.2) |
Vamos fazer agora a separação de variáveis:
| > |
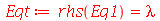 |
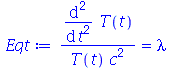 |
(1.7.2.1.3) |
| > |
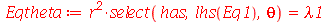 |
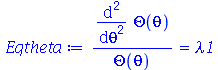 |
(1.7.2.1.4) |
| > |
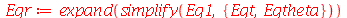 |
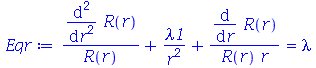 |
(1.7.2.1.5) |
A condição de contorno 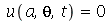 impõe que a constante
impõe que a constante 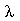 seja negativa pois quando ela é positiva ou nula, a equação Eqr não adimite soluções que se anulem para
seja negativa pois quando ela é positiva ou nula, a equação Eqr não adimite soluções que se anulem para 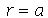 . Além disso, a variável
. Além disso, a variável 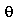 é periódica. Assim, vamos assumir que:
é periódica. Assim, vamos assumir que:
| > |
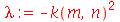 |
| > |
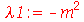 |
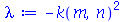 |
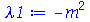 |
(1.7.2.1.6) |
A solução geral para Eqr a menos de uma constante multiplicativa é:
| > |
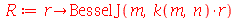 |
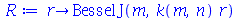 |
(1.7.2.1.7) |
| > |
 |
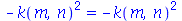 |
(1.7.2.1.8) |
A solução geral para 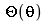 é:
é:
| > |
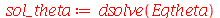 |
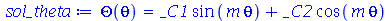 |
(1.7.2.1.9) |
| > |

 |
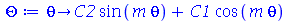 |
(1.7.2.1.10) |
A solução geral para 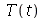 é:
é:
| > |
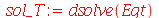 |
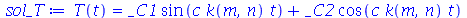 |
(1.7.2.1.11) |
| > |
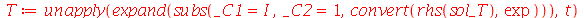 |
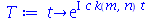 |
(1.7.2.1.12) |
Cálculo dos Modos Normais
Vamos agora analisar os modos normais da membrana circular. Os modos com 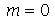 não dependem da variável
não dependem da variável 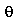 , isto é, eles são axialmente simétricos. Os modos com
, isto é, eles são axialmente simétricos. Os modos com 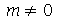 dependem da variável
dependem da variável 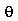 e em função disto veremos exemplos dos dois casos. A frequência do modo normal é:
e em função disto veremos exemplos dos dois casos. A frequência do modo normal é:
| > |
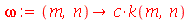 |
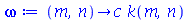 |
(1.7.2.2.1) |
Para que as condições de contorno sejam satisfeitas, temos que impor que 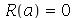 ou seja
ou seja 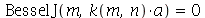 . Assim,
. Assim, 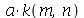 deve assumir valores que anulem a função de Bessel de ordem
deve assumir valores que anulem a função de Bessel de ordem 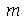 :
:
| > |
 |
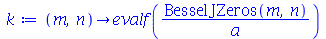 |
(1.7.2.2.2) |
A função 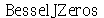 calcula o n-ésimo zero da função de Bessel de ordem
calcula o n-ésimo zero da função de Bessel de ordem 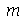 . Vamos agora definir os modos normais em funçao de
. Vamos agora definir os modos normais em funçao de 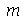 e
e 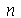 . Se
. Se 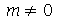 existe uma degenerescência de quarta ordem, isto é, podemos definir os seguintes modos normais:
existe uma degenerescência de quarta ordem, isto é, podemos definir os seguintes modos normais:
| > |
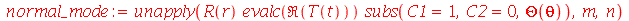 |
| > |
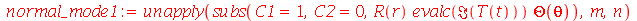 |
| > |
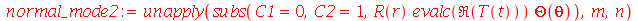 |
| > |
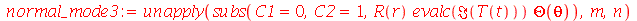 |
Os modos normais axialmente simétricos são os modos com 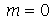 . Neste caso, a degenerescência é dupla, já que os modos
. Neste caso, a degenerescência é dupla, já que os modos 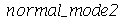 e
e 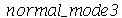 acima são nulos.
acima são nulos.
A solução geral é a superposição de todos os modos normais. A variável 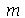 pode assumir qualquer valor inteiro de 0 a
pode assumir qualquer valor inteiro de 0 a 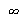 e
e 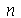 de 1 a
de 1 a 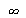 . Porém, para as condicões iniciais que estamos tratando aqui, a série de Fourier converge rapidamente, de forma que podemos truncar o somatório. As variáveis
. Porém, para as condicões iniciais que estamos tratando aqui, a série de Fourier converge rapidamente, de forma que podemos truncar o somatório. As variáveis 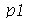 e
e 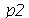 especificam o truncamento em
especificam o truncamento em 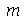 e
e 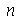 , respectivamente. Vamos separar os termos com
, respectivamente. Vamos separar os termos com 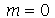 pois estes coeficientes seguem uma regra diferente dos coeficientes com
pois estes coeficientes seguem uma regra diferente dos coeficientes com 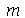 diferente de zero:
diferente de zero:
| > |


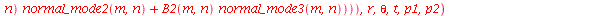 |
Os coeficientes 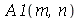 ,
, 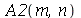 ,
, 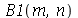 e
e 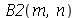 são constantes que dependem dos parâmetros
são constantes que dependem dos parâmetros 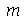 e
e 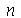 . Quando as condições iniciais são axialmente simétricas,
. Quando as condições iniciais são axialmente simétricas, 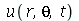 não depende de
não depende de 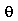 . Neste caso, temos que tomar
. Neste caso, temos que tomar 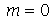 , o que é equivalente a tomar
, o que é equivalente a tomar 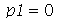 . A expressão de
. A expressão de 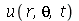 se reduz a:
se reduz a:
| > |
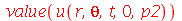 |
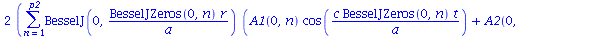
 |
(1.7.2.2.5) |
Animação dos Modos Normais
Vamos construir uma função para a membrana circular da mesma forma que foi construído para a membrana retangular:
| > |
 |
| > |
![animate_mode := proc (m, n) options operator, arrow; animate3d([r, theta, normal_mode(m, n)], r = 0 .. a, theta = 0 .. `+`(`*`(2, `*`(Pi))), t = 0 .. `*`(.99, `*`(evalf(`+`(`/`(`*`(2, `*`(Pi)), `*`(om...](images/curso8_614.gif)
![animate_mode := proc (m, n) options operator, arrow; animate3d([r, theta, normal_mode(m, n)], r = 0 .. a, theta = 0 .. `+`(`*`(2, `*`(Pi))), t = 0 .. `*`(.99, `*`(evalf(`+`(`/`(`*`(2, `*`(Pi)), `*`(om...](images/curso8_615.gif) |
Para fazer a animação de um determinado modo normal, temos que dar valores numéricos para os parâmetros 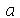 e
e 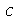 . Vamos supor que o raio é
. Vamos supor que o raio é 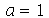 e
e 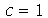 em um certo sistema de unidades:
em um certo sistema de unidades:
| > |
 |
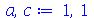 |
(1.7.2.3.1) |
Primeiro, vamos analisar o movimento do modos normais axialmente siméticos (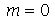 ). Vamos fazer a animação do modo <0,1>:
). Vamos fazer a animação do modo <0,1>:
| > |
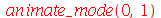 |
O primeiro modo axialmente simétrico não possui linha nodal, como era de se esperar. O segundo modo deve ter uma linha nodal:
| > |
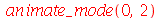 |
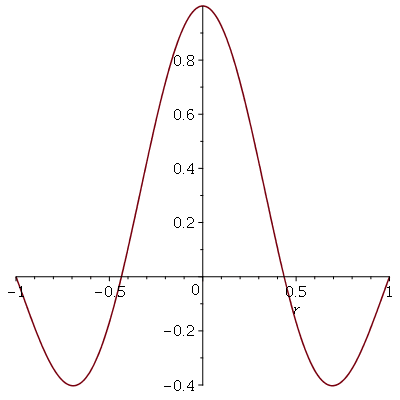
A linha nodal é um círculo cujo raio pode ser calculado da seguinte maneira. Observe que um corte vertical passando pelo centro do gráfico acima tem a seguinte forma:
| > |
 |
| > |
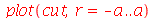 |
A posição inicial do modo <0,2> é a figura formada pela rotação do gráfico acima em torno do eixo vertical. É fácil ver pelo gráfico que, de maneira geral, a primeira linha nodal do modo <0,n> tem o raio  . No caso acima obtemos
. No caso acima obtemos 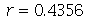 .
.
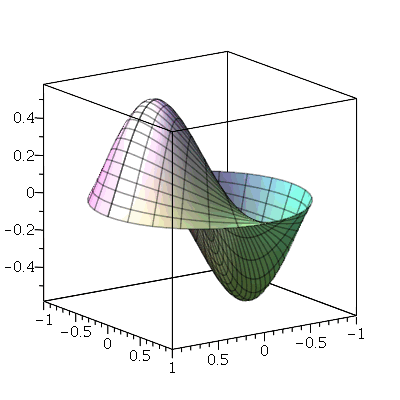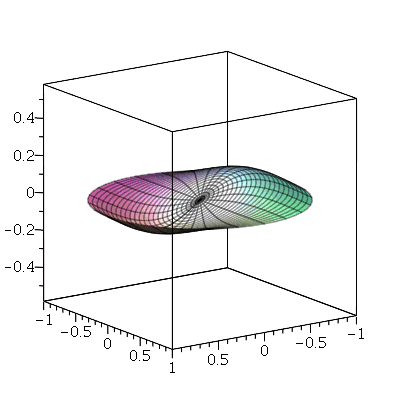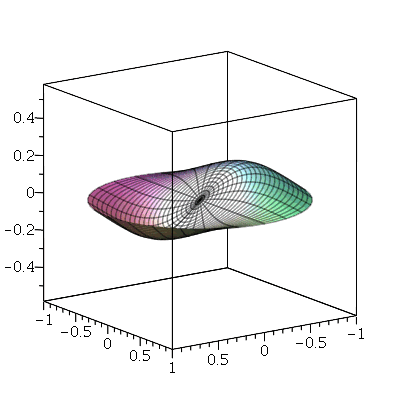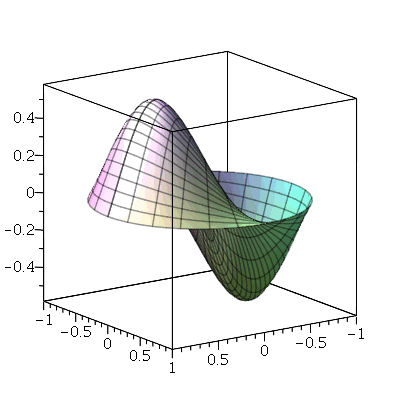
O primeiro modo normal não axialmente simétrico é o modo <1,1>:
| > |
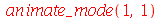 |
Neste caso, a linha nodal é uma reta passando pelo centro cujo ângulo é 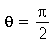 . Os modos normais com
. Os modos normais com 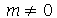 e
e 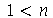 são de difícil visualização sem recursos de animação. Vejamos o modo <1,2>:
são de difícil visualização sem recursos de animação. Vejamos o modo <1,2>:
| > |
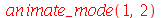 |
De maneira geral, o modo <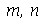 > tem
> tem 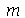 retas nodais passando pelo centro separadas entre si pelo ângulo
retas nodais passando pelo centro separadas entre si pelo ângulo 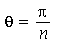 e
e 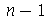 círculos de raios
círculos de raios ![r[p] = `/`(`*`(a, `*`(BesselJZeros(0, 1))), `*`(BesselJZeros(0, n)))](images/curso8_644.gif) , onde
, onde 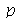 vai de 1 até
vai de 1 até 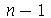 . As linhas nodais são mostradas pelo seguinte procedimento:
. As linhas nodais são mostradas pelo seguinte procedimento:
| > |
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_647.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_648.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_649.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_650.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_651.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_652.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_653.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_654.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_655.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_656.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_657.gif)
![nodal_lines := proc (m::posint, n::nonnegint) local ci, sl, p; global a, r; for p to n do ci[p] := plots[polarplot](`/`(`*`(a, `*`(BesselJZeros(0, p))), `*`(BesselJZeros(0, n)))) end do; for p to m do...](images/curso8_658.gif) |
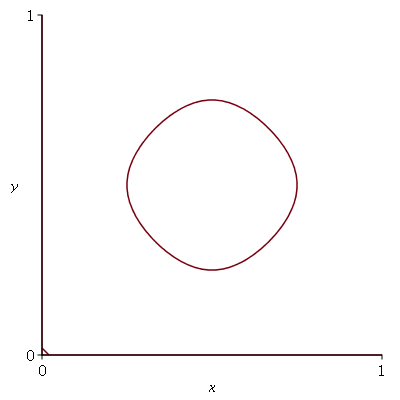
Por exemplo, o modo <2,3> tem as seguintes linha nodais:
| > |
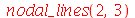 |
Observe que o círculo mais externo não deve ser contado como uma linha nodal, pois representa a borda da membrana.
Animação com Condições Iniciais
| > |
 |
| > |
 |
| > |
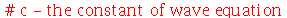 |
| > |
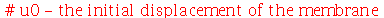 |
| > |
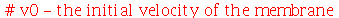 |
As constantes 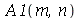 ,
, 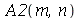 ,
, 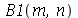 e
e 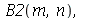 que aparecem na função
que aparecem na função 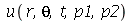 definida anteriormente, podem ser obtidas a partir das expressões teóricas derivadas a partir da inversão da série de Fourier:
definida anteriormente, podem ser obtidas a partir das expressões teóricas derivadas a partir da inversão da série de Fourier:
| > |
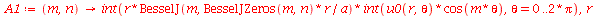
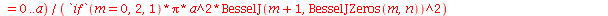
 |
| > |
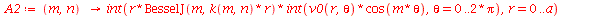
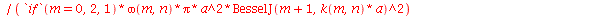 |
| > |
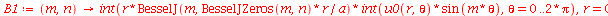
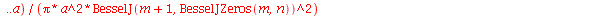 |
| > |
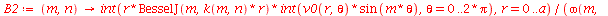
 |
A função a seguir faz a animação do movimento da membrana descrita pela função 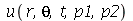 . O primeiro argumento do procedimento representa o tempo de oscilação, o seegundo argumento é o número
. O primeiro argumento do procedimento representa o tempo de oscilação, o seegundo argumento é o número 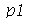 que representa a truncagem do somatório na variável
que representa a truncagem do somatório na variável 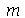 , o terceiro argumento é o número
, o terceiro argumento é o número 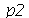 que representa a truncagem do somatório na variável
que representa a truncagem do somatório na variável 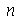 e o quarto é o número de frames na animação.
e o quarto é o número de frames na animação.
| > |
![animate_ic := proc (nt, p1, p2, frames0) options operator, arrow; plots:-animate3d([r, theta, value(u(r, theta, t, p1, p2))], r = 0 .. a, theta = 0 .. `+`(`*`(2, `*`(Pi))), t = 0 .. nt, coords = cylin...](images/curso8_689.gif)
![animate_ic := proc (nt, p1, p2, frames0) options operator, arrow; plots:-animate3d([r, theta, value(u(r, theta, t, p1, p2))], r = 0 .. a, theta = 0 .. `+`(`*`(2, `*`(Pi))), t = 0 .. nt, coords = cylin...](images/curso8_690.gif) |
Vamos ver dois exemplos com condições iniciais axialmente simétricas. O primeiro com velocidade inicial nula e o segundo com delocamento inicial nulo. Vamos tomar as seguintes condições iniciais:
| > |
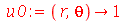 |
| > |
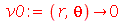 |
 |
 |
(1.7.2.4.2) |
Ou seja, a membrana está repouso na posição 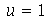 . Tomaremos o raio da membrana igual a 5:
. Tomaremos o raio da membrana igual a 5:
| > |
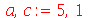 |
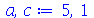 |
(1.7.2.4.3) |
Os coeficientes 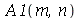 ,
, 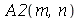 ,
, 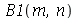 e
e 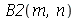 são:
são:
| > |
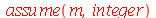 |
| > |
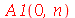 |
| > |
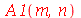 |
| > |
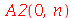 |
| > |
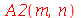 |
| > |
 |
| > |
 |
Vamos fazer a animação com duas oscilações dominantes e com . Uma vez que a condição inicial é axialmente simétrica, vamos tomar :
| > |
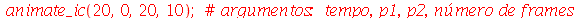 |
Podemos ver pela animação que a onda reflete na borda da membrana e se superpõe no centro, produzindo um propagação típica de ondas, como deveria ser. A reflexão na borda inverte o deslocamento da onda, já que a extremidade é fixa.
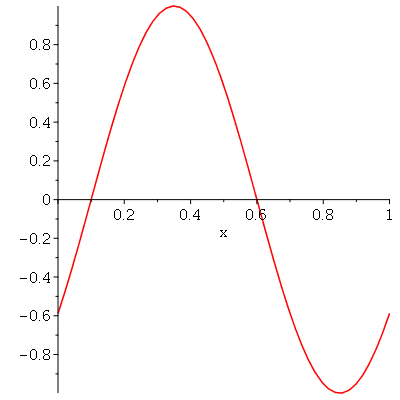
Vamos fazer a animação do movimento da membrana no caso em que ela está na posição horizontal e sofre um impulso de cima para baixo na região central. As condições iniciais são:
| > |
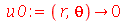 |
| > |
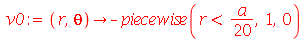 |
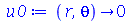 |
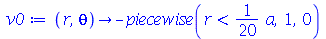 |
(1.7.2.4.5) |
A animação é obtida da através do comando:
| > |
 |
![]() é o nome da função indeterminada (opcional)
é o nome da função indeterminada (opcional) ![f(x, t) = `+`(`*`(_C3, `*`(exp(`*`(`^`(a, 2), `*`(_c[1], `*`(t)))), `*`(_C1, `*`(exp(`*`(`^`(_c[1], `/`(1, 2)), `*`(x))))))), `/`(`*`(_C3, `*`(exp(`*`(`^`(a, 2), `*`(_c[1], `*`(t)))), `*`(_C2))), `*`(...](images/curso8_30.gif)
![f(x, y) = `+`(`*`(_C1, `*`(exp(`*`(`^`(_c[1], `/`(1, 2)), `*`(x))), `*`(_C3, `*`(sin(`*`(`^`(`+`(_c[1], `-`(1)), `/`(1, 2)), `*`(y))))))), `*`(_C1, `*`(exp(`*`(`^`(_c[1], `/`(1, 2)), `*`(x))), `*`(_C4...](images/curso8_65.gif)
![f(x, y) = `+`(`*`(_C1, `*`(exp(`*`(`^`(_c[1], `/`(1, 2)), `*`(x))), `*`(_C3, `*`(sin(`*`(`^`(`+`(_c[1], `-`(1)), `/`(1, 2)), `*`(y))))))), `*`(_C1, `*`(exp(`*`(`^`(_c[1], `/`(1, 2)), `*`(x))), `*`(_C4...](images/curso8_66.gif)
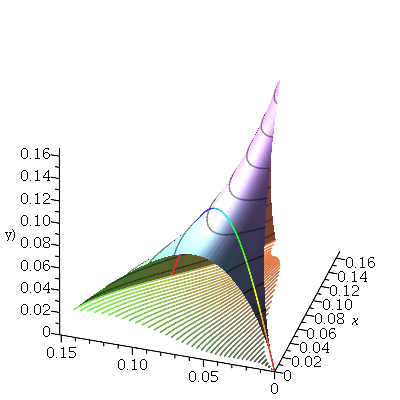
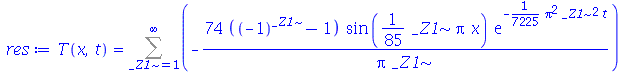
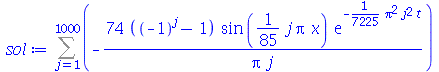


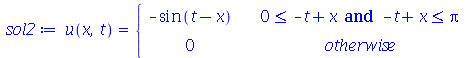
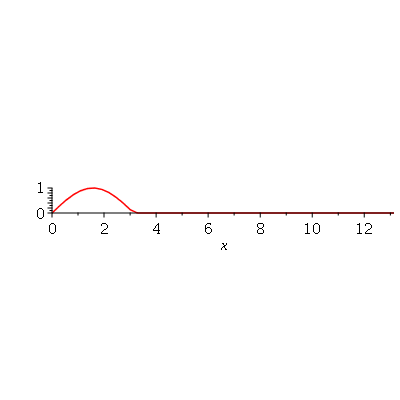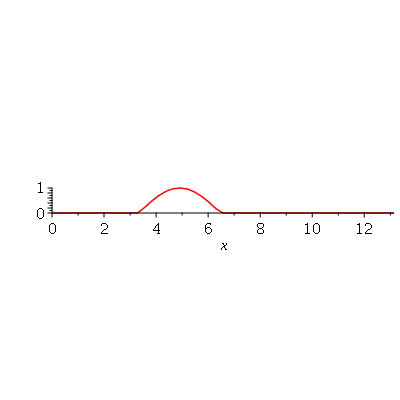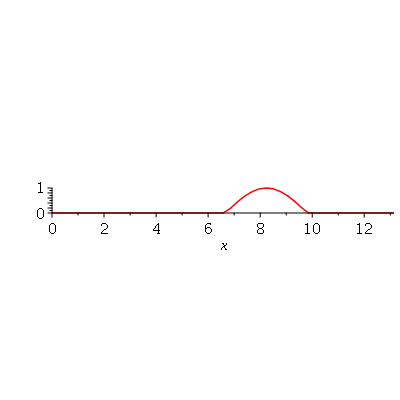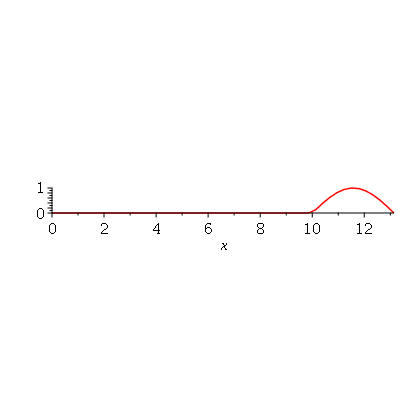
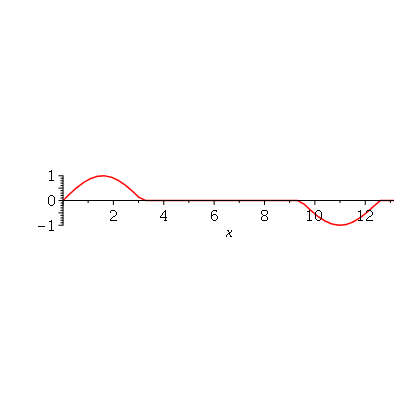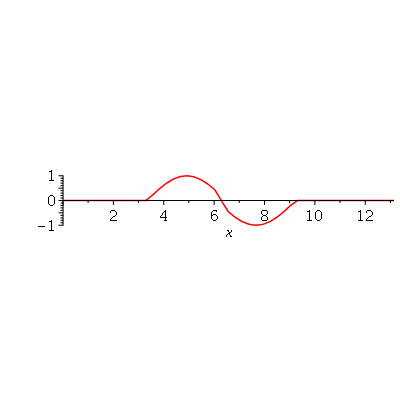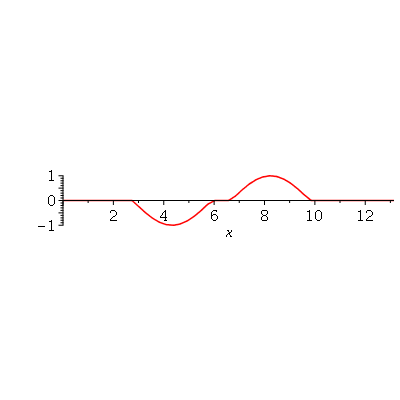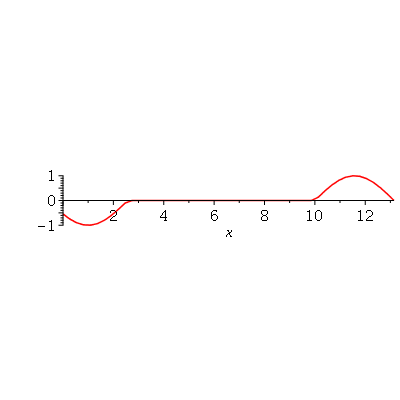
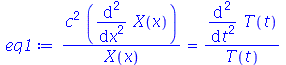
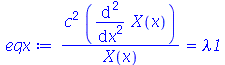
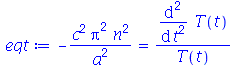
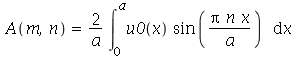 e
e 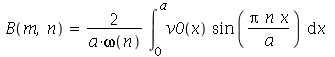 (veja referências sobre inversão de séries de Fourier, por exemplo, E. Butkov, Física Matemática, cap. 4).
(veja referências sobre inversão de séries de Fourier, por exemplo, E. Butkov, Física Matemática, cap. 4). 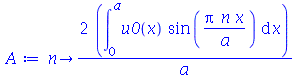
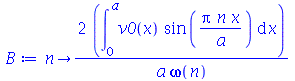
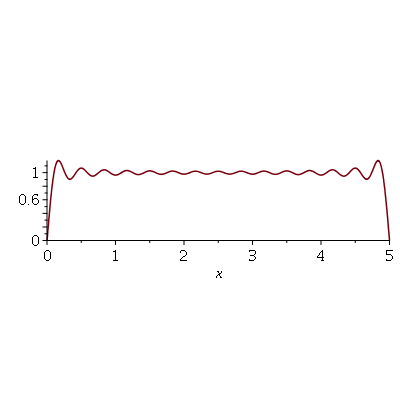
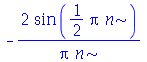
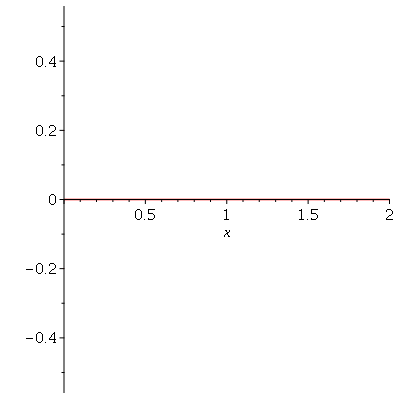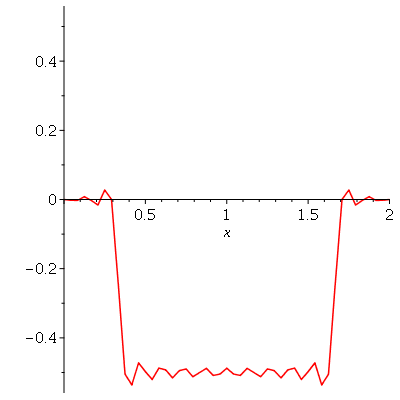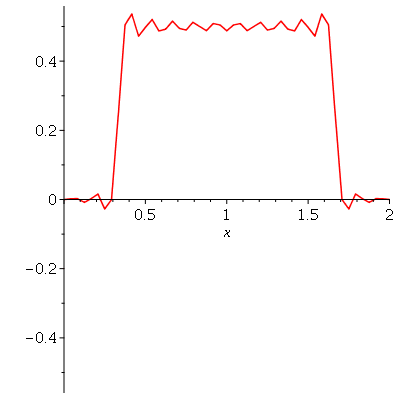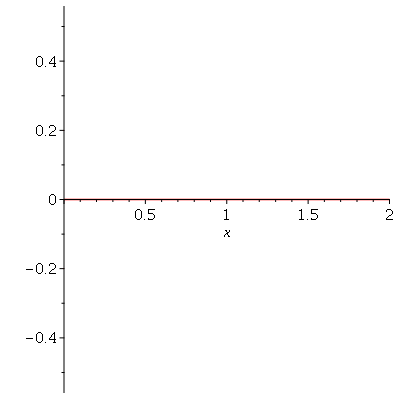
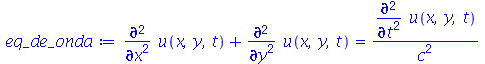
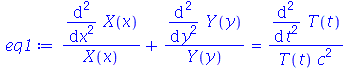
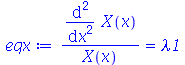
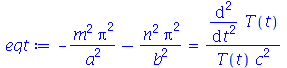
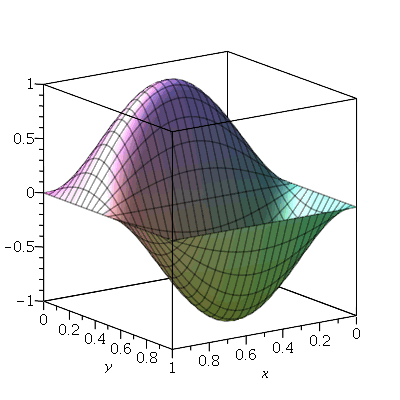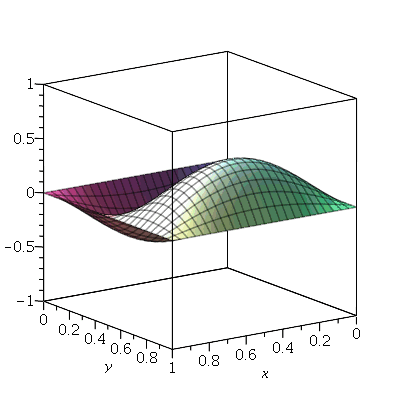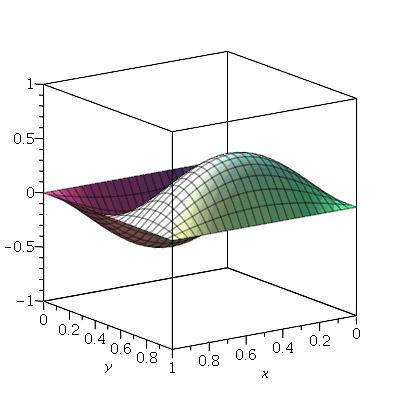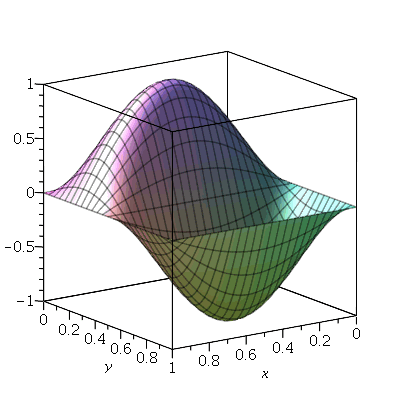
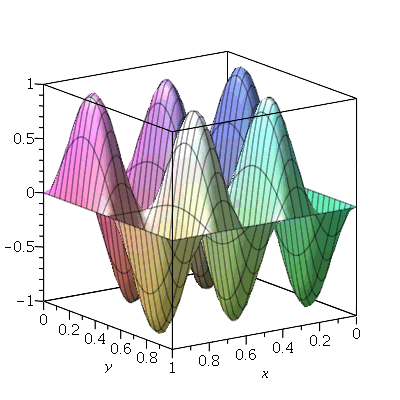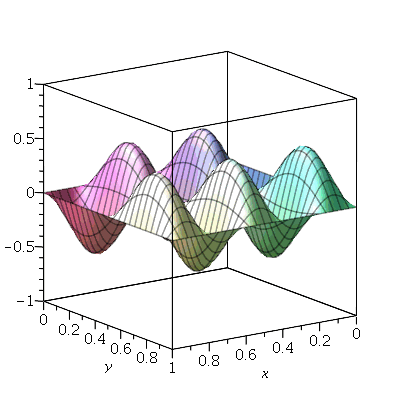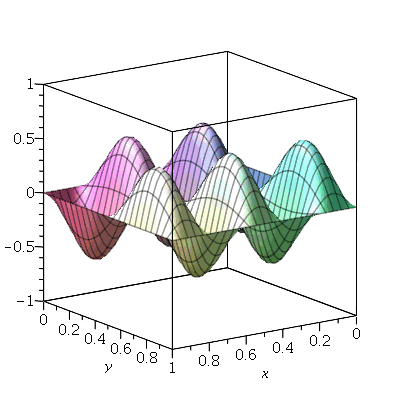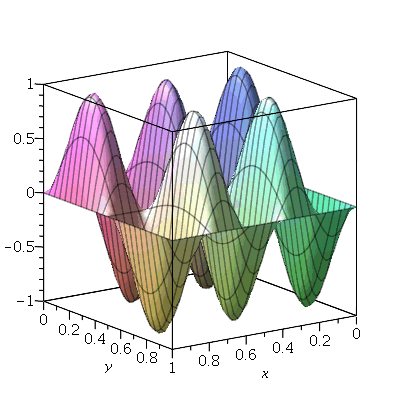
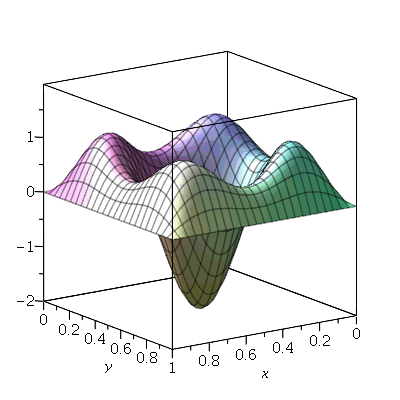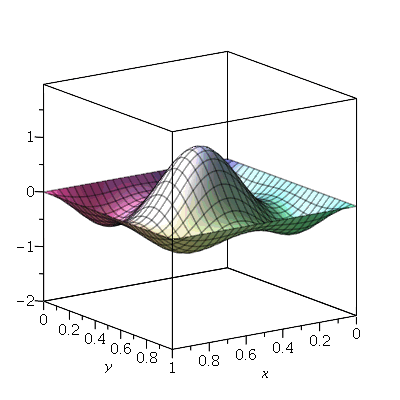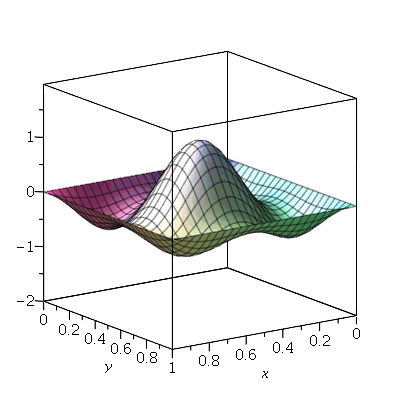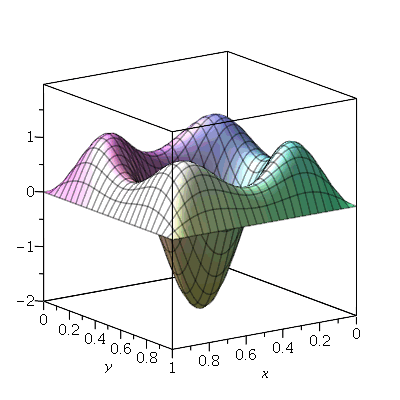
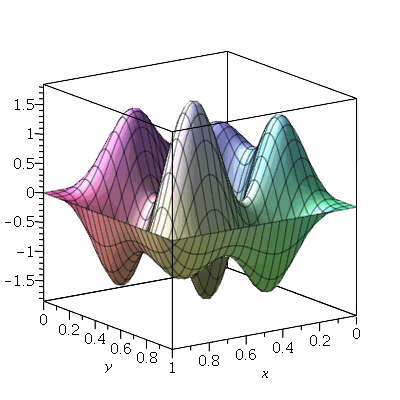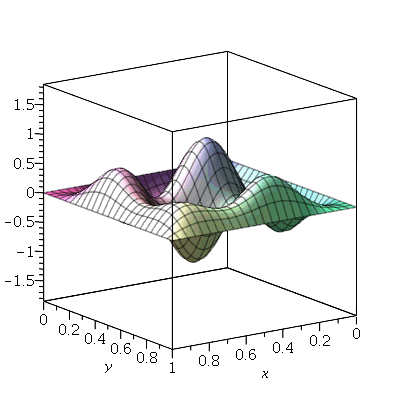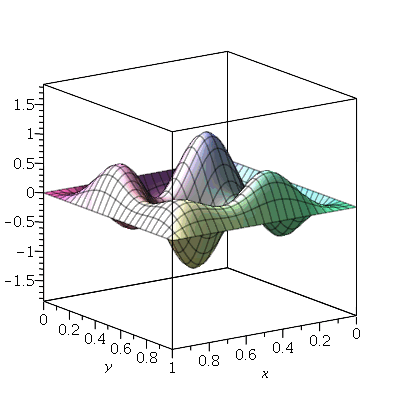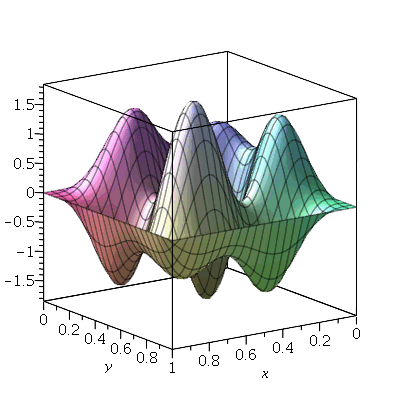
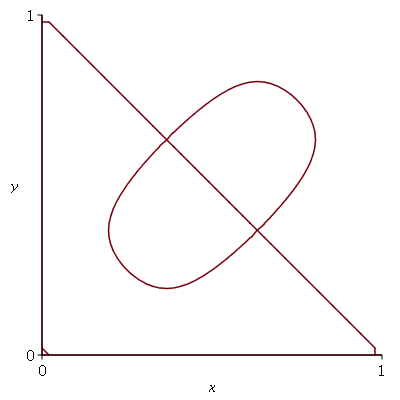
![A(m, n) = `+`(`/`(`*`(4, `*`(int(`*`(u0(x, y), `*`(sin(`/`(`*`(Pi, `*`(m, `*`(x))), `*`(a))), `*`(sin(`/`(`*`(Pi, `*`(n, `*`(y))), `*`(b)))))), [x = 0 .. a, y = 0 .. b]))), `*`(a, `*`(b))))](images/curso8_444.gif) e
e ![B(m, n) = `+`(`/`(`*`(4, `*`(int(`*`(v0(x, y), `*`(sin(`/`(`*`(Pi, `*`(m, `*`(x))), `*`(a))), `*`(sin(`/`(`*`(Pi, `*`(n, `*`(y))), `*`(b)))))), [x = 0 .. a, y = 0 .. b]))), `*`(a, `*`(b, `*`(omega(m, ...](images/curso8_445.gif) (veja referências sobre inversão de séries de Fourier).
(veja referências sobre inversão de séries de Fourier).