curso2.mw
Capítulo 2 Noções Básicas
Para obter os melhores resultados, este texto deverá ser lido junto com o uso do Maple, de forma que os exemplos possam ser testados. Neste caso, as dúvidas e as dificuldades ficarão mais visíveis. Antes de prosseguir, é fortemente recomendado que o usuário remova os resultados dos comandos (parte azul desta worksheet) e grave em um arquivo backup. Isto pode ser feito da seguinte forma: clique em Editar (ou Edit) no canto superior a esquerda, depois clique em Remova saída (remove output), depois clique em Da folha-de-trabalho (from worksheet). Após eliminar a parte azul, clique em Arquivo (File), depois Salvar como (save as), escolha o diretório e um nome novo para o arquivo, que deve ter extensão ".mw". Use este novo arquivo para suas modificações e salve sempre que possível. Evite lixo na worksheet apagando rascunho desnecessário (com ctrl del - veja hot keys no curso1) antes de fechar a sessão.
Números
O Maple usualmente trabalha com os números de maneira exata, isto é, nenhuma aproximação é feita. Veja por exemplo
| > |
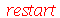 |
| > |
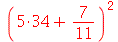 |
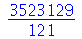 |
(1.1) |
o comando
restart
parece desnecessário, porém ele é útil quando re-executamos a folha-de-trabalho. O produto é executado com *, porém aparece na tela como um ponto 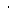 no meio da linha. Podemos notar que o resultado é um número racional. Para obter uma aproximação decimal, devemos usar o comando evalf (evaluate in floating point)
no meio da linha. Podemos notar que o resultado é um número racional. Para obter uma aproximação decimal, devemos usar o comando evalf (evaluate in floating point)
| > |
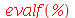 |
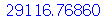 |
(1.2) |
O sinal de percentagem % guarda o valor do último resultado calculado, que não é necessariamente o resultado do comando imediatamente acima, pois na worksheet podemos processar os comandos numa ordem diferente da ordem que eles aparecem na tela. O último resultado tem 10 dígitos (valor default). Podemos calcular com mais dígitos significativos, por exemplo, com 50 dígitos (%% se refere ao penúltimo resultado)
| > |
](images/curso2_7.gif) |
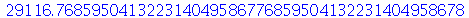 |
(1.3) |
Outra maneira de gerar resultados com casas decimais é entrar pelo menos um número decimal (lembre que o produto é com a tecla *, porém ele é opcional)
| > |
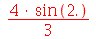 |
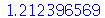 |
(1.4) |
Porém, como podemos aumentar o número de casas, se não estamos usando o comando evalf? Para isso devemos atribuir o número de dígitos desejado à variável Digits. Primeiro, vamos verificar seu valor default (para verificar o valor de uma variável, escreva o nome e dê enter), e depois vamos mudá-lo
| > |
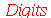 |
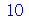 |
(1.5) |
| > |
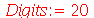 |
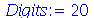 |
(1.6) |
Vejamos agora o número de Euler com vinte dígitos (entre com exp(1.), para colocar na forma de exponencial 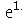 entre com exp, pressione ESC depois 1.)
entre com exp, pressione ESC depois 1.)
| > |
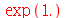 |
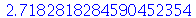 |
(1.7) |
No Maple, podemos trabalhar com números irracionais (para escrever 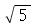 , use a forma sqrt(5)).
, use a forma sqrt(5)).
| > |
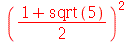 |
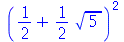 |
(1.8) |
| > |
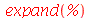 |
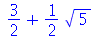 |
(1.9) |
Observe que a entrada não foi simplificada até que isto fosse pedido. Esta é uma regra do Maple. As expressões não são simplificadas a menos que o usuário exiga (através de comandos). Somente são feitas as simplificações mais elementares, envolvendo as operações aritméticas básicas. Por exemplo 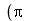 deve ser escrito Pi, com primeira letra maiúscula)
deve ser escrito Pi, com primeira letra maiúscula)
| > |
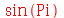 |
 |
(1.10) |
Vamos ver agora um exemplo mais elaborado (para Pi aparecer como  , escreva Pi com a primeira letra maiúscula e pressione ESC depois ENTER)
, escreva Pi com a primeira letra maiúscula e pressione ESC depois ENTER)
| > |
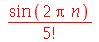 |
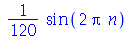 |
(1.11) |
Poderíamos achar que o resultado deveria ser zero, já que o seno de um múltiplo de Pi é zero. Com um pouco de reflexão mudaríamos de opinião, já que n é uma letra sobre a qual nada foi dito. Não é razoável esperar que o Maple assuma que ela é uma variável inteira. Para o Maple, ela é uma letra como qualquer outra. A princípio, todas estão em pé de igualdade. Isso pode ser mudado com o seguite comando
| > |
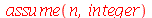 |
| > |
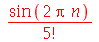 |
 |
(1.12) |
| > |
 |
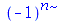 |
(1.13) |
De agora em diante, o Maple tratará n como uma variável inteira. Ela passa a ser mostrada na tela com um til, da forma ![`~`[n]](images/curso2_34.gif) , para o usuário saber que essa variável tem uma determinada propriedade atribuída pelo comando assume. É possível inibir o aparecimento do til nesse tipo de variáveis com o comando
, para o usuário saber que essa variável tem uma determinada propriedade atribuída pelo comando assume. É possível inibir o aparecimento do til nesse tipo de variáveis com o comando
| > |
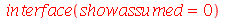 |
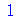 |
(1.14) |
| > |
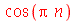 |
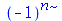 |
(1.15) |
Outro detalhe que podemos observar do último exemplo, é que o número  é escrito com P maiúsculo. A variável pi com p minúsculo não tem nenhuma relação com a constante matemática
é escrito com P maiúsculo. A variável pi com p minúsculo não tem nenhuma relação com a constante matemática  . Vamos retirar a declaração antes de continuar
. Vamos retirar a declaração antes de continuar
| > |
 |
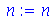 |
(1.16) |
No Maple, as aspas simples 'n' e as aspas duplas "n" têm funções diferentes. As aspas duplas são usadas para definir uma string, para manipulação de textos e nomes de arquivos e diretórios. As aspas simples são usadas para retardar a avaliação de uma variável. O comando 'n' vai retornar o nome n em vez do valor de n. O comando n:='n' faz com que o nome n seja atribuído a n, limpando a variável. É estranho mas dá para acostumar.
Agora, vamos ver um exemplo com números complexos. Queremos encontrar as raízes cúbicas de
| > |
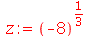 |
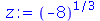 |
(1.17) |
Podemos ver que o Maple nada fez, ou melhor, não houve nenhuma simplificação do resultado. Assim, vamos pedir explicitamente
| > |
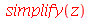 |
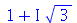 |
(1.18) |
A variável I (letra i maiúscula) representa 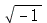 . O usuário pode mudar isto escolhendo outra variável, por exemplo J, através do comando interface(imaginaryunit=J). Os números complexos são sempre simplificados para a forma a+b I . Por exemplo
. O usuário pode mudar isto escolhendo outra variável, por exemplo J, através do comando interface(imaginaryunit=J). Os números complexos são sempre simplificados para a forma a+b I . Por exemplo
| > |
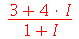 |
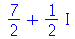 |
(1.19) |
Isso não ocorre se a expressão contiver uma letra. Por exemplo
| > |
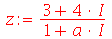 |
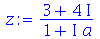 |
(1.20) |
Neste caso, devemos usar o comando evalc (evaluate in complex context). Vejamos
| > |
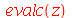 |
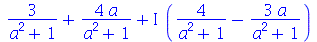 |
(1.21) |
Dentro do evalc, todas a letras são consideradas variáveis reais, exceto as variáveis que o usuário tenha declarado complexas através do comando assume. Podemos obter a parte real, imaginária e o módulo de z com a ajuda do evalc
| > |
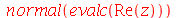 |
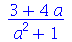 |
(1.22) |
| > |
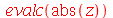 |
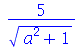 |
(1.23) |
Lembre que a variável I é reservada e portanto o usuário não pode fazer uma atribuição do tipo
| > |
 |
| Error, illegal use of an object as a name |
|
Exitem várias outras variáveis reservadas no Maple que não podem sofrer atribuição. A maioria está protegida e a mensagem de erro indica claramente onde está o problema. No caso caso da variável I, a mensagem de erro é enigmática.
Atribuição de um Nome para uma Expressão
A princípio, uma expressão não precisa ter um nome. Podemos nos referir a ela com o sinal %. Nas situações em que vamos nos referir a uma expressão diversas vezes, é melhor dar um nome a ela. Isto é feito com o comando de atribuição ``:=''. Por exemplo
| > |
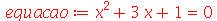 |
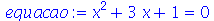 |
(2.1) |
| > |
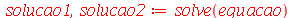 |
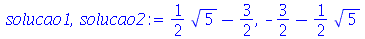 |
(2.2) |
O comando
solve
retorna uma sequência com dois resultados quando resolve uma equação de segunda ordem, por isso podemos fazer uma atribuíção simultânea em duas variáveis. Podemos confirmar que solução1 é de fato uma solução da equação
| > |
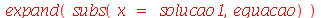 |
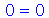 |
(2.3) |
Note que o sinal de igualdade = tem um papel bem diferente do sinal de atribuição :=. O sinal de igualdade não modifica o valor de uma variável. Vejamos
| > |
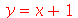 |
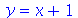 |
(2.4) |
O valor de y continua sendo ele próprio
| > |
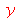 |
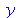 |
(2.5) |
Vejamos agora
| > |
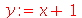 |
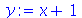 |
(2.6) |
| > |
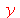 |
 |
(2.7) |
Como vimos anteriormente, para retirar a atribuição (''limpar a variável''), usa-se
| > |
 |
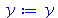 |
(2.8) |
De modo equivalente
| > |
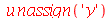 |
As aspas simples são necessárias, pois sem elas o comando unassign receberia o argumento x+1 e não teria como limpar 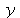 .
.
| > |
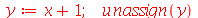 |
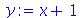 |
| Error, (in unassign) cannot unassign `x+1' (argument must be assignable) |
|
O último comando mostra como podemos colocar vários comando em uma mesma linha. Devemos separá-los por : (dois pontos) ou por ; (ponto e vígula). Para usar a maioria dos caracteres não-alfanuméricos no nome de uma variável, é necessário usar as crases, como mostra o exemplo
| > |
 |
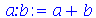 |
(2.9) |
No entando, o caracter _ não precisa de crases. Por exemplo
| > |
 |
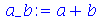 |
(2.10) |
Note que as crases têm uma função bem diferente das aspas simples. No Maple, um crase tem que ser fechada por uma crase e uma aspa simples tem que ser fechada por uma aspa simples.
Avaliação Completa
Vamos fazer atribuições em cadeia
| > |
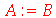 |
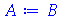 |
(3.1) |
| > |
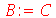 |
 |
(3.2) |
| > |
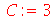 |
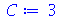 |
(3.3) |
Agora, observe o valor que o Maple retorna para a variável A
| > |
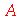 |
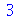 |
(3.4) |
O que aconteceu foi que A foi avaliado como B que por sua vez foi avaliado como C que foi avaliado como 3. Isso se chama avaliação completa de uma variável. Existem várias excessões a essa regra como veremos ao longo deste texto. Estas excessões são muito importantes. Podemos adiantar uma, a saber, no comando abaixo a variável A não será avaliada
| > |
 |
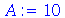 |
(3.5) |
Caso A tivesse sido avaliado retornando o valor 3, teríamos o comando 3 :=10, o que não é admitido. Existe uma maneira de retardar a avaliação de uma variável. Sabemos que o comando A vai retornar 10. Porém, podemos retardar esta avaliação e no comando seguinte forçar a avaliação completa
| > |
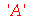 |
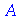 |
(3.6) |
| > |
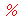 |
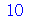 |
(3.7) |
Isso explica porque o comando A:='A' limpa a variável A. Já tinha sido explicado anteriormente, porém a ficha pode demorar para cair. O recurso de retardar a avaliação, seja de uma variável, seja de um comando, é utilizado com muita frequência.
Tipos de Objetos
Para usar o Maple de maneira eficiente, é necessário conhecer a forma de alguns objetos desta linguagem. Outro nome para objetos do Maple comumente usado é estrutura de dados. Os principais são as listas, conjuntos, arrays, sequências e tabelas. Vários comandos do Maple têm estes objetos como resultado. Podemos precisar selecionar um elemento do resultado e, para isto, é necessário compreender a estruturas destes objetos. O resultado do comando solve pode ser uma sequência de raízes de uma equação, como vimos acima. Uma sequência é uma série de objetos separados do vírgula. Vejamos outro exemplo (as crases são usadas para nomes com caracteres não alfanuméricos, no caso o espaço em branco)
| > |
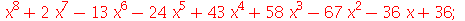 |
| > |
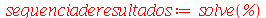 |
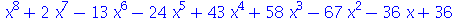 |
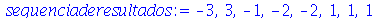 |
(4.1) |
O resultado do comando solve foi uma sequência de raízes, sendo que as raízes repetidas aparecem tantas vezes quanto for a multiplicidade. No caso acima, a raíz 1 tem multiplicidade 3 e a raíz -2 tem multiplicidade 2. Podemos, agora, colocar esta sequência de raízes na forma de outros objetos. Por exemplo, na forma de uma lista (lista é uma sequência entre colchetes)
| > |
![listaderesultados := [sequenciaderesultados]](images/curso2_102.gif) |
![[-3, 3, -1, -2, -2, 1, 1, 1]](images/curso2_103.gif) |
(4.2) |
Outra possibilidade é armazenar as raízes na forma de um conjunto (conjunto é uma sequência entre chaves)
| > |
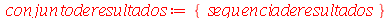 |
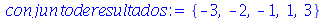 |
(4.3) |
Cada objeto tem sua característica própria. Podemos ver que a lista mantêm o ordenamento das raízes e não elimina as repetições. Por sua vez, o conjunto não respeita o ordenamento e elimina as repetições. O conjunto acima tem 5 elementos enquanto que a lista tem 8 elementos, número este que deve coincidir com o grau do polinômio. Para selecionar um elemento de um objeto do Maple, deve-se usar a seguinte notação
OBJETO[posição do elemento]
Por exemplo, vamos selecionar o quarto elemento da sequência de soluções
| > |
![sequenciaderesultados[4]](images/curso2_106.gif) |
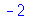 |
(4.4) |
O último elemento da lista de soluções
| > |
![listaderesultados[-1]](images/curso2_108.gif) |
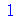 |
(4.5) |
Neste último exemplo, podemos sempre selecionar o último elemento mesmo sem ter contado à mão (ou por inspeção visual) quantos elementos o objeto tem. Um número negativo indica que a contagem é feita a partir do final da lista: -1 indica o último elemento, -2 o penúltimo, e assim por diante. O comando nops fornece o tamanho da lista ou do conjunto. Para memorizar o nome do comando é bom saber que nops é o acrônimo de number of operands. Vamos usar com frequência o nome ``operando'' para nos referir a ``elemento''. Vamos nos colocar o seguinte problema: queremos saber qual é o polinômio que tem as mesmas raízes que o polinômio acima, porém todas com multiplicidade 1. Ou seja, sabemos que as raízes do polinômio que queremos achar são
| > |
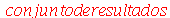 |
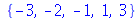 |
(4.6) |
Temos então que construir o polinômio (x+3)*(x+2)*(x+1)... . A maneira mais simples de resolver este problema é escrever explicitamente o seguinte produto
| > |
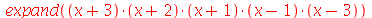 |
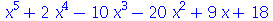 |
(4.7) |
Caso o número de raízes seja grande, não é conveniente usar este método, pois ele será trabalhoso e podemos cometer erros. Vejamos uma outra forma de resolver o problema (o operador 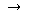 é obtido com - seguindo de > )
é obtido com - seguindo de > )
| > |
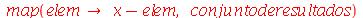 |
 |
(4.8) |
| > |
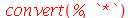 |
 |
(4.9) |
| > |
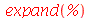 |
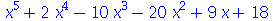 |
(4.10) |
Este método é o mesmo não importa o número de raízes. Um erro comum de ser cometido no primeiro método é usar x-2 no lugar de x+2. O segundo método não corre este risco. Aqui foi usado o comando map (abreviação de mapping). Ele está associado às estruturas de dados. Todos os comandos que usamos até agora atuavam em um único elemento. No entanto, quando estamos lidando com estrutura de dados ou objetos com muitos elementos, precisamos aplicar comandos ou funções em todos os elementos da estrutura. O comando que faz isso é o map. No exemplo acima, queremos somar x a cada elemento do conjunto de soluções. A notação é 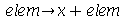 . Esta operação deve ser realizada em todos os elementos do conjunto de soluções. O primeiro argumento do comando map deve ser a lei transformação. O segundo argumento tem que ser o conjunto ou qualquer objeto com vários elementos. O resultado foi que cada elemento foi somado a x. Falta mais um passo para obter o polinômio, que é converter o conjunto em produto. O produto é especificado no Maple como `*`. As crases são necessárias, pois o asterisco é um caracter não alfanumérico. O comando convert espera que o seu segundo argumento seja um nome. O asterisco não é um nome, mas sim o operador de multiplicação. As crases fazem com que ele seja apenas um nome, ou um caracter como qualquer outra letra. Podemos converter uma lista em um conjunto e vice-versa
. Esta operação deve ser realizada em todos os elementos do conjunto de soluções. O primeiro argumento do comando map deve ser a lei transformação. O segundo argumento tem que ser o conjunto ou qualquer objeto com vários elementos. O resultado foi que cada elemento foi somado a x. Falta mais um passo para obter o polinômio, que é converter o conjunto em produto. O produto é especificado no Maple como `*`. As crases são necessárias, pois o asterisco é um caracter não alfanumérico. O comando convert espera que o seu segundo argumento seja um nome. O asterisco não é um nome, mas sim o operador de multiplicação. As crases fazem com que ele seja apenas um nome, ou um caracter como qualquer outra letra. Podemos converter uma lista em um conjunto e vice-versa
| > |
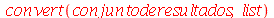 |
![[-3, -2, -1, 1, 3]](images/curso2_123.gif) |
(4.11) |
Os conjuntos são objetos inspirados nos conjuntos usados na Matemática. Podemos fazer a união, interseção e subtração de conjuntos com os comandos union, intersect e minus. Por exemplo
| > |
 |
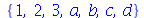 |
(4.12) |
| > |
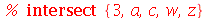 |
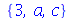 |
(4.13) |
| > |
 |
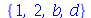 |
(4.14) |
Os conjuntos e as listas que têm uma certa regra de formação podem ser gerados com o comando seq (abreviação de sequence). Por exemplo, o conjunto dos 10 primeiros números primos
| > |
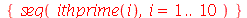 |
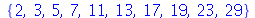 |
(4.15) |
A lista dos dez primeiros números da forma 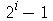
| > |
![[seq(`+`(`^`(2, i), `-`(1)), i = 1 .. 10)]](images/curso2_133.gif) |
![[1, 3, 7, 15, 31, 63, 127, 255, 511, 1023]](images/curso2_134.gif) |
(4.16) |
A lista das derivadas de x*ln(x) em relação a x até ordem 5 (o comando x$2 retorna a sequência x,x que é usado pelo comando diff para calcular a derivada segunda)
| > |
![[seq(diff(`*`(x, `*`(ln(x))), `$`(x, i)), i = 1 .. 5)]](images/curso2_135.gif) |
![[`+`(ln(x), 1), `/`(1, `*`(x)), `+`(`-`(`/`(1, `*`(`^`(x, 2))))), `+`(`/`(`*`(2), `*`(`^`(x, 3)))), `+`(`-`(`/`(`*`(6), `*`(`^`(x, 4)))))]](images/curso2_136.gif) |
(4.17) |
Vimos como selecionar um único elemento de uma estrutura de dados. Agora, como podemos obter um sub-conjunto de um conjunto ou uma sub-lista de uma lista? A notação para obter sub-listas ou sub-conjuntos é
OBJETO[ a .. b ]
onde a é a posição do primeiro elemento e b é a posição do último elemento da parte que queremos selecionar. Por exemplo
| > |
![lista1 := [a, b, c, d, e]](images/curso2_137.gif) |
![[a, b, c, d, e]](images/curso2_138.gif) |
(4.18) |
| > |
![sublista := lista1[2 .. 4]](images/curso2_139.gif) |
![[b, c, d]](images/curso2_140.gif) |
(4.19) |
Resolvendo Equações Algébricas
O principal comando para resolver equações algébricas é o comando
solve
:
| > |
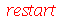 |
| > |
 |
 |
(5.1) |
| > |
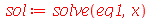 |
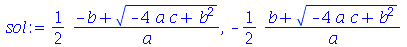 |
(5.2) |
Note que a solução é uma sequência. Para ter acesso à primeira solução use a notação ![sol[1]](images/curso2_146.gif) . Se o objetivo é apenas isolar um parâmetro, o comando mais conveniente é
isolate
:
. Se o objetivo é apenas isolar um parâmetro, o comando mais conveniente é
isolate
:
| > |
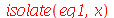 |
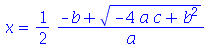 |
(5.3) |
Note que o resultado é uma equação. Para encontrar as soluções inteiras de equações algébricas devemos usar o comando
isolve
(acrônimo de integer solve):
| > |
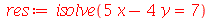 |
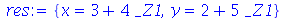 |
(5.4) |
Para resolver equações recursivas devemos usar o comando
rsolve
(acrônimo de recursive solve):
| > |
 |
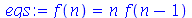 |
(5.5) |
| > |
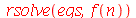 |
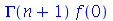 |
(5.6) |
A função GAMMA é definida como 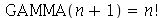 , onde
, onde 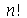 é o fatorial de
é o fatorial de 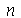 .
.
| > |
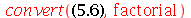 |
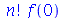 |
(5.7) |
Uma equação tem dois operandos que podem ser selecionados com os comandos
rhs
e
lhs
, acrônimo de right hand side e left hand side repectivamente. Para colocar a equação abaixo na forma padrào
| > |
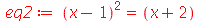 |
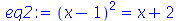 |
(5.8) |
podemos usar o seguinte comando:
| > |
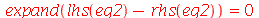 |
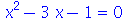 |
(5.9) |
Exercícios
1. Encontre a centésima casa decimal do número  e da razão áurea. [Sugestão: tente achar a quarta cada decimal do número
e da razão áurea. [Sugestão: tente achar a quarta cada decimal do número  . Depois de conseguir responder corretamente este caso, que é facilmente visualizável, você estará pronto para o caso mais desafiador.]
. Depois de conseguir responder corretamente este caso, que é facilmente visualizável, você estará pronto para o caso mais desafiador.]
2. Usando o comando seq, crie uma lista de equações da forma ![[x[1] = 1, x[2] = 2, x[3] = 3, x[4] = 4, x[5] = 5, x[6] = 6, x[7] = 7, x[8] = 8, x[9] = 9, x[10] = 10]](images/curso2_166.gif) e atribua à variável L. Usando o comando map, obtenha a partir de L, uma nova lista com os termos que estão no lado direito das equações. A partir do resultado, converta em produto através do comando convert e confira o resultado com o comando factorial.
e atribua à variável L. Usando o comando map, obtenha a partir de L, uma nova lista com os termos que estão no lado direito das equações. A partir do resultado, converta em produto através do comando convert e confira o resultado com o comando factorial.
3. Os primeiros números da sequência de Fibonacci são 1,1,2,3,5,8,13. O próximo é 21 que é obtido somando os dois anteriores 8+13. Use o Help on Line para achar comandos que gerem esta sequência. Crie uma lista com os 10 primeiros números.
4. Use o Help on Line para achar um comando que gere todas as permutações da lista [a,b,c] e atribua o resultado à variável L. Use o comando Search do pacote ListTools para encontrar a posição da lista [c,a,b] em L. Verifique o resultado usando o comando L[i], onde i é a posição retornada pelo Search.
5. Use o Help on Line para achar um comando que gere todos os subconjuntos do conjunto {a,b,c,d} e atribua o resultado à variável C. Use o comando nops para calcular o número de elemento de S e verifique se é igual a 2 elevado ao número de elementos do conjunto original. Use o comando minus para retirar o conjunto vazio do resultado. Use o comando select e a função 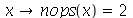 , para selecionar os subconjuntos com dois elementos. A função deve ser o primeiro argumento do comando select. [Sugestão: tente descobrir o nome do "conjunto dos subconjuntos de um conjunto" em Inglês, por exemplo, no Google. Em Português, o nome é "conjunto potência" ou "conjunto das partes".]
, para selecionar os subconjuntos com dois elementos. A função deve ser o primeiro argumento do comando select. [Sugestão: tente descobrir o nome do "conjunto dos subconjuntos de um conjunto" em Inglês, por exemplo, no Google. Em Português, o nome é "conjunto potência" ou "conjunto das partes".]
6. Resolva a equação x^8+2*x^7-13*x^6-24*x^5+43*x^4+58*x^3-67*x^2-36*x+36=0 e atribua o resultado à variável sols. Use os comandos seq, simplify, subs e nops para verificar com um único comando composto que todas as soluções estão corretas. Cada solução deve ser substituída na equação e simplificada. O resultado final deve ser uma sequência de 8 zeros.
7. (a) Use o Help on Line para achar um comando que resolva numericamente o sistema não-linear de equações 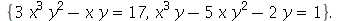
(b) Use o Help on Line para achar um comando que faça o gráfico simultâneo das curvas geradas pelos pontos 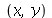 que satisfazem cada uma das equações do ítem (a) junto com o ponto-solução
que satisfazem cada uma das equações do ítem (a) junto com o ponto-solução 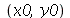 em destaque (use o resultado de (a)).
em destaque (use o resultado de (a)).
8. Gere um conjunto com os 8 primeiros números primos da forma 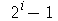 . [Sugestão: gere um conjunto
. [Sugestão: gere um conjunto 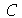 suficientemente grande com os números números da forma
suficientemente grande com os números números da forma 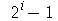 e use o comando select(type,C,prime). Use o Help on Line para entender o funcionamento do comando
select
para selecionar elementos de uma estrutura de dados]
e use o comando select(type,C,prime). Use o Help on Line para entender o funcionamento do comando
select
para selecionar elementos de uma estrutura de dados]
9. (a) Seja ![L1 := [1, 2]](images/curso2_174.gif) e
e ![L2 := [3, 4]](images/curso2_175.gif) (listas). Concatene
(listas). Concatene 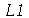 e
e 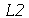 , isto é, crie uma nova lista tendo os elementos tanto de
, isto é, crie uma nova lista tendo os elementos tanto de 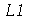 quanto de
quanto de 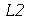 .
.
(b) Suponha que 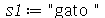 ,
, 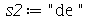 e
e 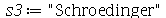 . Use o Help on Line para achar um comando que contatene os strings
. Use o Help on Line para achar um comando que contatene os strings 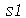 ,
, 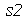 e
e 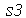 .
.
10.
(a) Gere uma lista aleatória com 20 números inteiros entre -10 e 20.
(b) Remova todos os números duplicados.
(c) Selecione da lista os números divisíveis por 2 (Sugestão use o comando
select
junto com
type
Procure pelo "tipo" "par", even em Inglês)
(d) Selecione da lista os números divisíveis por 3
(e) Selecione da lista os números divisíveis por 2 e 3
(e) Selecione da lista os números divisíveis por 2 ou 3
(f) Selecione os números maiores do que 5
(g) Remova os elementos divisíveis por 5.
11. Ache a maior raiz da equação 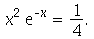 Note que a função exponencial
Note que a função exponencial 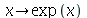 também pode ser expressa por
também pode ser expressa por 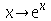 . Neste caso o "e" não é escrito em itálico. Quando o usuário escreve errado, aparece na forma
. Neste caso o "e" não é escrito em itálico. Quando o usuário escreve errado, aparece na forma 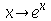 . Isso vale para as outras funções implementadas internamente no Maple, como
. Isso vale para as outras funções implementadas internamente no Maple, como  (função seno) e
(função seno) e 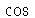 (função cosseno), isto é, estas funções não são apresentadas em itálico. Prestar atenção neste tipo de detalhe ajuda a evitar erros, principalmente para quem não está familiarizado com a língua inglesa.
(função cosseno), isto é, estas funções não são apresentadas em itálico. Prestar atenção neste tipo de detalhe ajuda a evitar erros, principalmente para quem não está familiarizado com a língua inglesa.
![]() no meio da linha. Podemos notar que o resultado é um número racional. Para obter uma aproximação decimal, devemos usar o comando evalf (evaluate in floating point)
no meio da linha. Podemos notar que o resultado é um número racional. Para obter uma aproximação decimal, devemos usar o comando evalf (evaluate in floating point) ![]() entre com exp, pressione ESC depois 1.)
entre com exp, pressione ESC depois 1.) ![]() , use a forma sqrt(5)).
, use a forma sqrt(5)). ![]() deve ser escrito Pi, com primeira letra maiúscula)
deve ser escrito Pi, com primeira letra maiúscula) ![]() , escreva Pi com a primeira letra maiúscula e pressione ESC depois ENTER)
, escreva Pi com a primeira letra maiúscula e pressione ESC depois ENTER) ![]() , para o usuário saber que essa variável tem uma determinada propriedade atribuída pelo comando assume. É possível inibir o aparecimento do til nesse tipo de variáveis com o comando
, para o usuário saber que essa variável tem uma determinada propriedade atribuída pelo comando assume. É possível inibir o aparecimento do til nesse tipo de variáveis com o comando ![]() é escrito com P maiúsculo. A variável pi com p minúsculo não tem nenhuma relação com a constante matemática
é escrito com P maiúsculo. A variável pi com p minúsculo não tem nenhuma relação com a constante matemática ![]() . Vamos retirar a declaração antes de continuar
. Vamos retirar a declaração antes de continuar ![]() . O usuário pode mudar isto escolhendo outra variável, por exemplo J, através do comando interface(imaginaryunit=J). Os números complexos são sempre simplificados para a forma a+b I . Por exemplo
. O usuário pode mudar isto escolhendo outra variável, por exemplo J, através do comando interface(imaginaryunit=J). Os números complexos são sempre simplificados para a forma a+b I . Por exemplo