Introdução
A sintaxe para gerar gráficos em 2 dimensões é:
plot( f(x), x = a .. b, opções)
onde f(x) é uma função de uma variável e a..b é o intervalo de variação da variável x. As opções são da forma:
nome da opção = tipo da opção
A lista completa dos nomes das opções e seus tipo pode ser obtida através do help on line com o comando ?
plot,options
. Um exemplo é color=blue. As principais são
axes = boxed, frame, none, normal
caption = "texto para a legenda global"
color = black, red, green, blue, "SpringGreen", "Turquoise" - veja
plot/colornames
gridlines = true, false - coloca uma malha sobre o gráfico
labels = [x,y] - nomes para os labels
legend = "texto para a legenda por gráfico"
linestyle = solid, dot, dash, dashdot, longdash, spacedash, spacedot
size = [largura,altura] - tamanho do gráfico
style = line, point, polygon (patchnogrid), polygonoutline (patch)
symbol = asterisk, box, circle, cross, diagonalcross, diamond, point, solidbox, solidcircle, soliddiamond - tipo de pontos para a curva ou gráfico
symbolsize = 10, 11, ... - tamanho do ponto do gráfico
thickness = 1, 2, ... - grossura da linha do gráfico
tickmarks = [30,40] - número de marcações nos eixos x e y
title = "Título do gráfico"
titlefont = ["ROMAN", 15], ["HELVETICA",20], ["COURIER", 10], ["ARIAL", 18]
As opções servem para se obter os efeitos desejados em cada gráfico. Vamos ver alguns exemplos com vários tipos de opções. Primeiro, vamos definir a função esférica de Bessel a partir da função cilíndrica de Bessel:
| > |
 |
 |
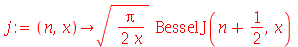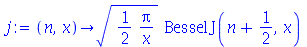(1.2.1.1) |
Agora, vamos fazer o gráfico da função de ordem zero com o título "Função Esférica de Bessel", com o nome `j(0,x)` no eixo vertical e controlando o número de marcações no eixo x e no eixo y:
| > |
 |
Note que `j(0,x)` está entre crases, pois a variável no eixo vertical tem que ser um nome (tipo name) e, por possuir caracteres não-alfanuméricos, precisa das crases. Por sua vez, o título deve ser um texto (tipo string), portanto deve vir entre aspas duplas.
Para visualizar melhor, podemos introduzir uma malha sobre o gráfico:
| > |
 |
Agora, vamos ver outros tipos de gráficos em 2 dimensões.
Gráficos de Funções Parametrizadas
A sintaxe dos gráficos de funções parametrizadas é:
plot( [x(t), y(t), t = a .. b], opções)
onde as opções são da mesma forma do comando plot usual. A lista completa pode ser obtida com o comando ?plot,options.
Como exemplo, vamos fazer um espiral:
| > |
![plot([`*`(t, `*`(cos(`+`(`*`(2, `*`(Pi, `*`(t))))))), `*`(t, `*`(sin(`+`(`*`(2, `*`(Pi, `*`(t))))))), t = 0 .. 10], scaling = constrained, axes = none)](images/curso5_25.gif) |
Note que a opção scaling=constrained serve para mostrar a característica circular desta figura.
Gráficos em Coordenadas Polares
A sintaxe dos gráficos de funções em coordenadas polares é:
polarplot( r(theta), theta = a .. b, opções)
onde as opções são da mesma forma do comando plot usual. A lista completa pode ser obtida com o comando ?
plot,options
.
É possível também fazer gráficos em coordenadas polares parametrizados. A sintaxe é:
polarplot( [r(x), theta(x), x = a .. b], opções)
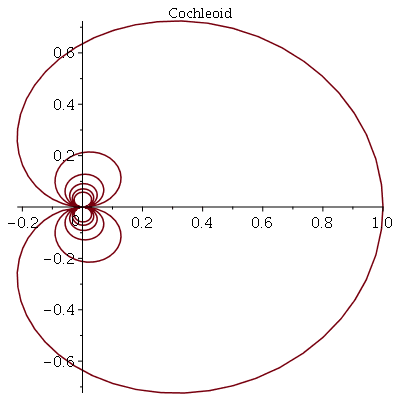
Como exemplo, vamor fazer o gráfico da figura conhecida por Cocheloid.
| > |
![plot([`/`(`*`(sin(t)), `*`(t)), t, t = `+`(`-`(`*`(6, `*`(Pi)))) .. `+`(`*`(6, `*`(Pi)))], coords = polar, title =](images/curso5_27.gif) |
 |
|
Gráficos de Funções Contínuas por Partes
As funções contínuas por partes são definidas com o comando piecewise. As funções definidas desta forma podem ser diferenciadas e integradas. Por exemplo, vamos definir uma função cujo gráfico tem a forma de uma barreira. A função é descrita por:
Assim, podemos usar o comando piecewise da seguinte forma:
| > |
 |
 |
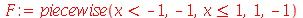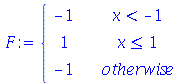(1.2.4.1) |
| > |
 |
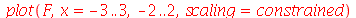Observe que as descontinuidades do gráfico foram unidas por retas verticais. Estas retas podem ser eliminadas com a opção discont=true:
| > |
 |
 |
|
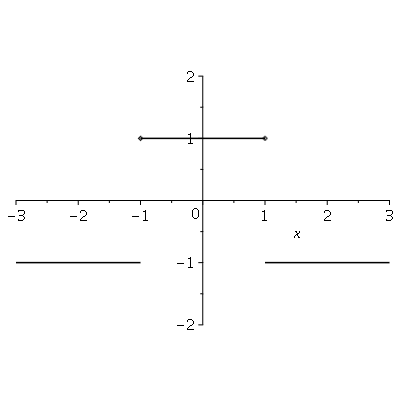Gráficos de Pontos Isolados
Podemos fazer gráficos de pontos isolados com a opção style=point:
| > |
 |
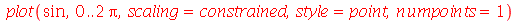Quando atribuimos um gráfico a uma variável, podemos manipular com a estrutura dos gráficos e ver quais pontos o Maple escolheu para gerar o gráfico em questão.
| > |
  |
Estes pontos não são igualmente espaçados, pois nas regiões onde a curvatura do gráfico é maior, o Maple escolhe mais pontos, como podemos verificar no gráfico anterior. Vamos fazer os mesmo gráfico, porém vamos nós mesmos escolher os pontos de forma que fiquem igualmente espaçados. Vamos gerar estes pontos com o comando seq:
| > |
![sin_points := seq(evalf([`*`(`+`(`*`(2, `*`(Pi, `*`(i)))), `/`(1, 30)), sin(`*`(`+`(`*`(2, `*`(Pi, `*`(i)))), `/`(1, 30)))], 3), i = 1 .. 30)](images/curso5_40.gif) |
Vamos colocar a sequência de pontos em uma lista, e fazer o gráfico com a opção style=points:
| > |
![plot([sin_points], scaling = constrained, style = point)](images/curso5_46.gif) |
Vejamos outro exemplo:
| > |
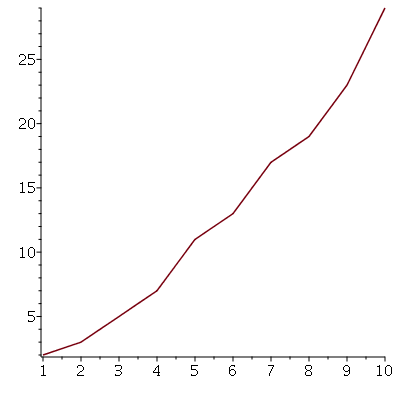
![pontos := seq([i, ithprime(i)], i = 1 .. 10)](images/curso5_48.gif) |
![[1, 2], [2, 3], [3, 5], [4, 7], [5, 11], [6, 13], [7, 17], [8, 19], [9, 23], [10, 29]](images/curso5_49.gif) |
(1.2.5.2) |
| > |
![plot([pontos], style = point)](images/curso5_50.gif) |
Sem a opção style=point, os pontos são unidos por retas:
| > |
![plot([pontos])](images/curso5_52.gif) |
 |
|
Gráficos de Funções Definidas Implicitamente
Vejamos um exemplo:
| > |
 |
| > |
![implicitplot(`+`(`+`(`*`(`^`(x, 2)), `-`(x), `/`(1, 4), `*`(`^`(y, 2)), `-`(y)), `/`(1, 4)) = 1, x = -1 .. 2, y = -1 .. 2, grid = [30, 30], color = black)](images/curso5_55.gif) |
 |
|
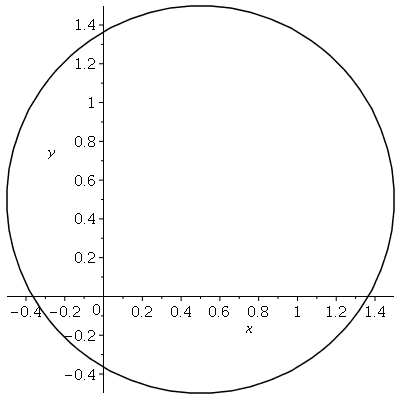Gráficos em 3 Dimensões
Introdução
A sintaxe dos gráficos em 3 dimensões é:
plot3d( f(x,y), x = a .. b, y = c .. d, opções)
onde f(x,y) é uma função de duas variáveis, a .. b é o intervalo para o eixo x e c .. d é o intervalo para o eixo y. As opções são da forma
nome da opção = tipo da opção
A lista completa dos nomes das opções e seus tipo pode ser obtida através do help on line com o comando ?
plot3d/option
. As principais são
- axes=boxed, normal, frame, none
- contours = 10, 11, ... - número de curvas de contorno
- gridstyle=rectangular, triangular
- labeldirections=[x, y, z]; x,y,z=horizontal, vertical
- labels=[x, y, z]; x,y,z podem ser textos
- linestyle=olid, dot, dash, dashdot, longdash, spacedash, spacedot
- orientation=[theta, phi, psi]; por exemplo [45, 45, 0]
- scaling= unconstrained, constrained
- shading=xy, xyz, z, zgrayscale, zhue, none
- style=surface (patchnogrid), surfacewireframe (patch), contour, surfacecontour (patchcontour), wireframe (line), wireframeopaque (hidden), point
- symbol=asterisk, box, circle, cross, diagonalcross, diamond, point, solidsphere, sphere
- tickmarks=[m, n, p]; por exemplo [20,20,10]
- title="Título para o gráfico"
- view=zmin..zmax ou [xmin..xmax, ymin..ymax, zmin..zmax]
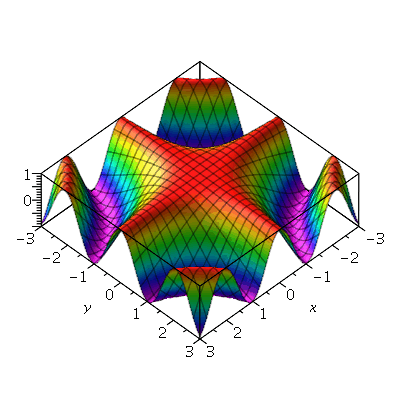
Vejamos alguns exemplos:
| > |
![plot3d(cos(`*`(x, `*`(y))), x = -3 .. 3, y = -3 .. 3, grid = [49, 49], axes = boxed, scaling = constrained, shading = zhue)](images/curso5_57.gif) |
 |
|
| > |
 |
 |
|
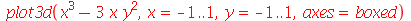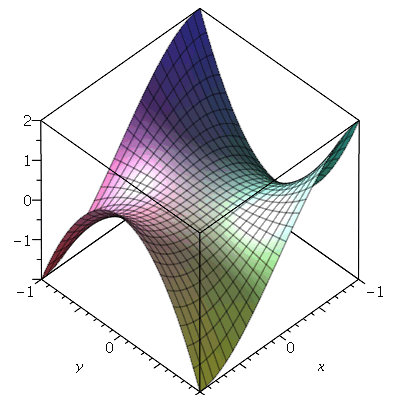Gráficos de Funções Parametrizadas
A sintaxe dos gráficos de funções parametrizadas em 3 dimensões é:
plot3d( [x(t,s), y(t,s), z(t,s)], t = a .. b, s = c .. d, opções)
onde as opções são da mesma forma do comando plot3d usual. A lista completa pode ser obtida com o comando ?
plot3d/option
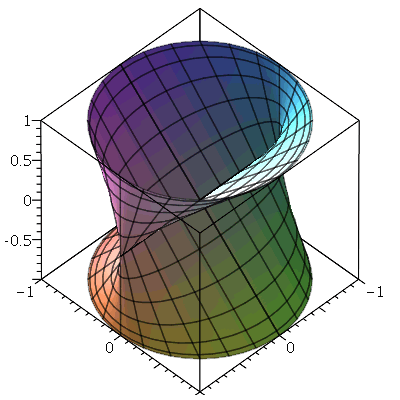
. Note que a lista não inclui o intervalo das variáveis t e s, como ocorre no comando equivalente em 2 dimensões. Vamos ver um exemplo:
| > |
![plot3d([sin(t), `*`(cos(t), `*`(sin(s))), sin(s)], t = `+`(`-`(Pi)) .. Pi, s = `+`(`-`(Pi)) .. Pi)](images/curso5_61.gif) |
 |
|
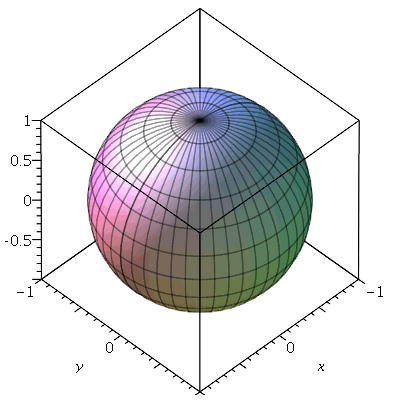
Gráficos em Coordenadas Esféricas
A sintaxe dos gráficos de funções em coordenadas esféricas é:
sphereplot( r(theta,phi), theta = a .. b, phi = c .. d, opções)
É possível também fazer gráficos de funções em coordenadas esféricas parametrizadas. A sintaxe é:
sphereplot( [r(t,s), theta(t,s), phi(t,s)], t = a .. b, s = c .. d, opções)
O comando sphereplot está dentro do pacote plots. Vamos ver um exemplo do primeiro caso:
| > |
 |
| > |
 |
 |
|
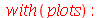Exibindo vários Gráficos Simultaneamente
Para exibir dois ou mais gráficos simultaneamente, podemos usar o comando plot ou plot3d colocando as expressões de cada gráfico dentro de uma lista (entre colchetes) ou em um conjunto (entre chaves). Vimos um exemplo no início deste capítulo. Desta forma, todas a opções usadas serão comuns a todos os gráficos.
Para fazer gráficos com opções diferentes e mostrá-los na mesma tela, temos que tomar outro caminho. Cada gráfico deve ser feito independentemente e atribuído a uma variável. Para mostrar os gráficos juntos, devemos usar o comando display ou display3d dependendo se forem gráficos em 2 ou 3 dimensões. As variáveis devem ser colocadas dentro de uma lista ou um conjunto. Estes comandos estão dentro do pacote plots. Vejamos um exemplo:
| > |
 |
| > |
 |
| > |
 |
| > |
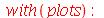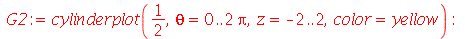![display([G1, G2], scaling = constrained)](images/curso5_69.gif) |
Para ver um dos gráficos isoladamente, basta avaliar a variável onde o gráfico foi guardado. Por exemplo, para ver a esfera:
| > |
 |
 |
|
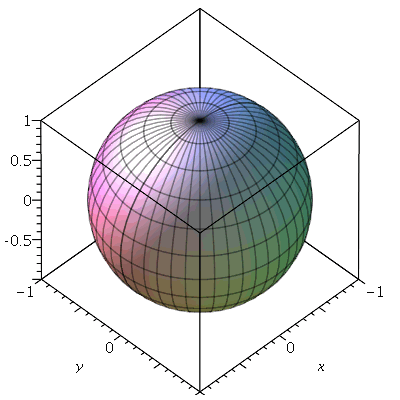Animando Gráficos em duas ou três Dimensões
Além de permitir fazer gráficos numa mesma tela simultaneamente, o Maple permite que vários gráficos sejam exibidos em sequência, gerando o efeito de animação. Para fazer animação de gráficos em coordenadas cartesianas com todas as opções em comum, podemos usar os comandos animate e animate3d. Vejamos um exemplo:
| > |
 |
| > |
 |
Para disparar a animação devemos clicar no gráfico e depois na tecla play. O comando animate gera tantos gráficos quanto for o valor da opção frames. Os valores que a variável t assume, depende do valor de frames. No caso acima, t assumiu os valores 
, 
, 
. Observe que t assumiu 12 valores, sendo que o valor 
e 
geram o mesmo gráfico. Isso faz com que a animação tenha sempre uma rápida parada quando um ciclo se completa. A maneira de evitar isto, é tomar o intervalo para t de 0 até 
.
Uma maneira alternativa de fazer a animação é usar a seguinte sintaxe:
| > |
![animate(plot, [sin(`+`(`*`(2, `*`(Pi, `*`(`+`(x, t)))))), x = 0 .. 1], t = 0 .. 1, frames = 12)](images/curso5_89.gif) |
Note que o valor de 
é mostrado parte superior. A vantagem desta sintaxe é que ela permite o uso de outros comandos do pacote plots. Por exemplo
| > |
 |
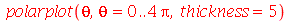O comando acima gera um gráfico polar para um intervalo fixo. Para fazer a animação em um intervalo variável:
| > |
![animate(polarplot, [theta, theta = 0 .. t, thickness = 5], t = 0 .. `+`(`*`(4, `*`(Pi))))](images/curso5_94.gif) |
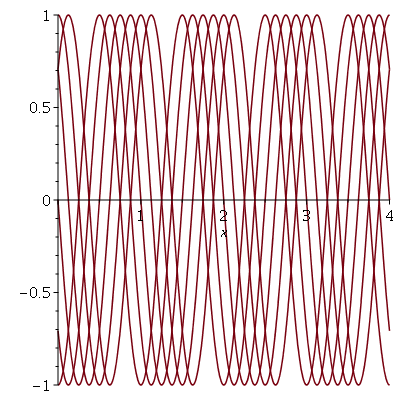
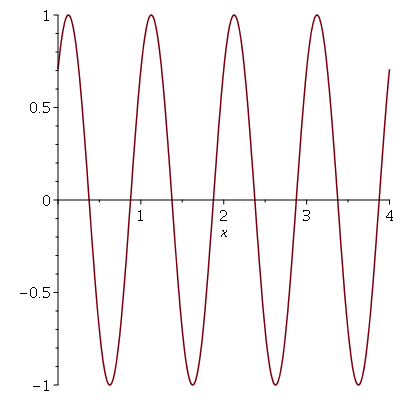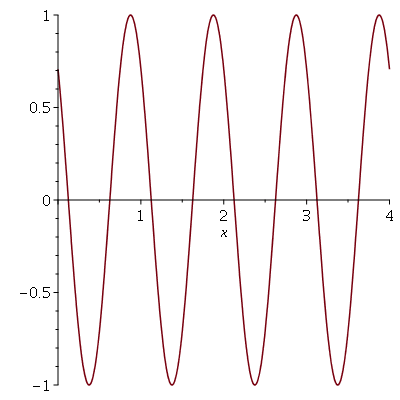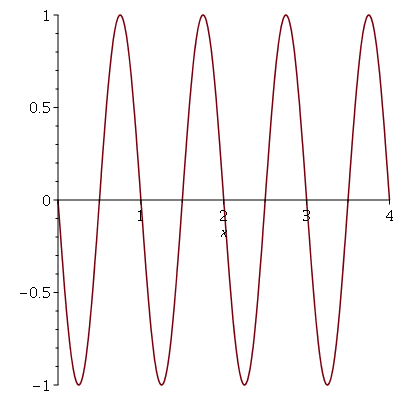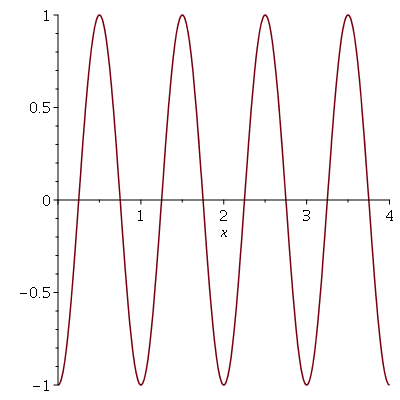
Para fazer a animação de outros tipos de gráficos sem ser em coordenadas cartesianas, temos que usar um método mais elaborado. Cada gráfico deve ser feito independentemente e atribuído a uma variável. Cada comando de atribuição deve ser terminado com dois pontos ``:''. Para mostrar os gráficos em sequência, devemos usar o comando display ou display3d, dependendo se forem gráficos em 2 ou 3 dimensões, com a opção insequence=true. O comando for é muito útil neste contexto, pois podemos gerar vários gráficos com um único comando. A título de exemplo, vamos fazer a mesma animação anterior sem usar o comando animate:
| > |
![for i to 6 do P[i] := plot(sin(`+`(`*`(2, `*`(Pi, `*`(`+`(x, `*`(`/`(1, 8), `*`(i)))))))), x = 0 .. 4) end do; -1](images/curso5_96.gif) |
| > |
![display({seq(P[i], i = 1 .. 6)})](images/curso5_97.gif) |
 |
|
| > |
![display([seq(P[i], i = 1 .. 6)], insequence = true)](images/curso5_99.gif) |
 |
|
Colocando Textos em Gráficos
Os comandos usuais de gerar gráficos colocam uma série de textos no gráfico. Este é o caso do nome das coordenadas, do título do gráfico entre outros. Podemos escolher as fontes através das opções font, titlefont, axesfont e labelfont. Porém, para modificar a posição destes textos, é necessário proceder de outra forma. Devemos usar os comandos textplot e textplot3d, que têm as seguintes sintaxe:
textplot( [coord-x, coord-y, `texto`] )
e
textplot3d( [coord-x, coord-y, coord-z, `texto`] )
onde coord-x é um número especificando a posição x do centro do texto. O mesmo com relação a coord-y e coord-z. Estes comandos geram um gráfico com o texto desejado na posição especificada. Com o comando display ou display3d juntamos estes gráficos-textos com o gráfico das funções em questão.
Vejamos um exemplo de composição de vários gráficos-textos. Cada gráfico será atribuido a uma variável e os comandos serão terminados com dois-pontos para evitar que informações desnecessárias sejam mostradas na tela. Somente o comando display será terminado com ponto-e-vírgula:
| > |
 |
| > |
 |
| > |
![G3 := textplot([3.0, .8, `J(0,x)`], font = [](images/curso5_103.gif) |
| > |
 |
| > |
 |
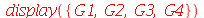Para exibir letras gregas é necessário usar a fonte symbol.
Salvando Gráficos em Arquivos e Imprimindo Gráficos
A maneira mais fácil de imprimir um gráfico é clicar com o mouse no gráfico, clicar o botão direito do mouse e exportar para o formato desejado e depois imprimir.
Também é possível imprimir através de comandos. Para imprimir gráficos no formato PostScript, temos que modificar o valor da variável plotdevice para ps, e direcionar a saida para um arquivo. Isto deve ser feito com o comando interface:
| > |
 |
 |
(1.7.1) |
| > |
 |
O gráfico do último comando foi enviado para o arquivo graf1.ps, e pode ser impresso numa impressora PostScript. Uma maneira alternativa de enviar gráficos para um arquivo é usando o comando plotsetup. Vamos mostrar mais um exemplo, mas nesse caso vamos tirar a caixa retangular que o Maple coloca no gráfico enviado para o arquivo, e vamos apresentá-lo na orientação usual (portrait em vez de landscape que é o default)
| > |
 |
Para voltar a mostrar o gráfico na worksheet novamente, o valor de plotdevice deve ser modificado para inline ou win:
| > |
 |
 |
(1.7.2) |
Para imprimir gráficos em outros formatos, veja o help on line de
plot,device
e
interface
.
Manipulando Gráficos
O pacote plottools tem vários comandos para manipulação com gráficos além de diversos comandos para criar objetos gráficos. Estes comandos não mostram o gráfico. O comando display do pacote plots deve ser usado em conjunto. Por exemplo, podemos criar um cone com a ponta na origem, de raio 1/2 e altura 2 com o comando cone:
| > |
 |
| > |
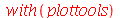![C := cone([0, 0, 0], `/`(1, 2), 2); -1](images/curso5_119.gif) |
| > |
 |
| > |
 |
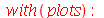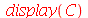Agora, vamos girar este cone de 
em relação ao eixo y:
| > |
 |
. 
![[-2 .. 2]](images/curso5_4.gif){kind=small}
é 
junto com as envoltórias. A curva 
na cor azul e as envoltórias em vermelho. Devemos colocar as funções em uma lista (colchetes quadrados) com as cores correspondentes na opção color. ![plot([F, exp(`+`(`-`(`*`(`^`(x, 2))))), `+`(`-`(exp(`+`(`-`(`*`(`^`(x, 2)))))))], x = -2 .. 2, color = [blue, red, red])](images/curso5_9.gif){kind=small}
![[1, 1, 1]](images/curso5_14.gif){kind=small}
com raio 5 e com raio de meridiano 3. Nesse caso vamos usar um comando especial do pacote plottools. ; -1](images/curso5_15.gif){kind=small}
](images/curso5_16.gif){kind=small}
![[.209, .207], [.418, .406], [.628, .588], [.838, .743], [1.05, .865], [1.26, .952], [1.47, .995], [1.67, .995], [1.88, .952], [2.09, .865], [2.30, .743], [2.51, .588], [2.72, .406], [2.93, .207], [3.1...](images/curso5_41.gif){kind=small}
![[.209, .207], [.418, .406], [.628, .588], [.838, .743], [1.05, .865], [1.26, .952], [1.47, .995], [1.67, .995], [1.88, .952], [2.09, .865], [2.30, .743], [2.51, .588], [2.72, .406], [2.93, .207], [3.1...](images/curso5_42.gif){kind=small}
![[.209, .207], [.418, .406], [.628, .588], [.838, .743], [1.05, .865], [1.26, .952], [1.47, .995], [1.67, .995], [1.88, .952], [2.09, .865], [2.30, .743], [2.51, .588], [2.72, .406], [2.93, .207], [3.1...](images/curso5_43.gif){kind=small}
![[.209, .207], [.418, .406], [.628, .588], [.838, .743], [1.05, .865], [1.26, .952], [1.47, .995], [1.67, .995], [1.88, .952], [2.09, .865], [2.30, .743], [2.51, .588], [2.72, .406], [2.93, .207], [3.1...](images/curso5_44.gif){kind=small}
![[.209, .207], [.418, .406], [.628, .588], [.838, .743], [1.05, .865], [1.26, .952], [1.47, .995], [1.67, .995], [1.88, .952], [2.09, .865], [2.30, .743], [2.51, .588], [2.72, .406], [2.93, .207], [3.1...](images/curso5_45.gif){kind=small}
