


Next: Discussion
Up: Specifying the System
Previous: Specifying the System
We now set up a simulation of the quantum neural network. We specify as
inputs the initial
 polarizations of each of two quantum
dot molecules, spatially far enough from each other that they do not
interact directly, but sharing the same substrate.
The system output
polarizations of each of two quantum
dot molecules, spatially far enough from each other that they do not
interact directly, but sharing the same substrate.
The system output
 represents a combination of the basic
states of polarization, say
represents a combination of the basic
states of polarization, say  and
and  . To define
a training rule we have to define a scalar function of the system output
whose value is thresholded to decide if the desired behavior has been reproduced (a quantum logic gate, for example).
In [4] the polarization of the first molecule at the final
time is arbitrarily taken. Thus, the probability amplitude for the first
molecules final state to be equal to the
. To define
a training rule we have to define a scalar function of the system output
whose value is thresholded to decide if the desired behavior has been reproduced (a quantum logic gate, for example).
In [4] the polarization of the first molecule at the final
time is arbitrarily taken. Thus, the probability amplitude for the first
molecules final state to be equal to the  state is computed
(give by
state is computed
(give by
 ) and the signal of the following expression
considered:
) and the signal of the following expression
considered:
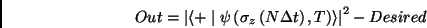 |
(11) |
if  the network is considered to be trained. To achieve this goal, an
Error Function is defined and a gradient descent algorithm was used
for training:
the network is considered to be trained. To achieve this goal, an
Error Function is defined and a gradient descent algorithm was used
for training:
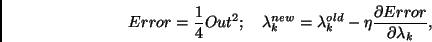 |
(12) |
where
![\begin{displaymath}
\frac{\partial Error}{\partial \lambda _{k}}=\frac{1}{2} Ou...
...lambda _{k}}\langle +\mid \psi \rangle ^{*}\right] \right]
\end{displaymath}](img108.png) |
(13) |
We shall emphasize that it is possible to train purely quantum gates such as
a phase shift, because the network is quantum mechanical.



Next: Discussion
Up: Specifying the System
Previous: Specifying the System
Gilson Giraldi
2002-07-02